Numerical Methods -- Solutions to an Ordinary Differential Equation -- Module 6

---

Index

1. 1. Euler’s Method
2. 2. Runge-Kutta Method (or Euler’s Modified Method)

---

1. Euler’s Method

https://www.youtube.com/watch?v=ukNbG7muKho

Concept

Euler’s method is the simplest numerical method for solving an initial value problem of the form:

$\frac{dy}{dt}=f(t,y),y(t_0)=y_0$

It approximates the solution by moving a small step size $h$ forward in time and using the derivative $f(t,y)$ to update the value of $y$.

---

Formula

If you know $y(t_n)$ and want to compute $y(t_{n+1})$ with a step $h$:

$y_{n+1}=y_n+h{f}^{\prime }(t_n,y_n)$

where $h$ is the step size.

---

Pros and Cons

• Pros:

  • Very simple to implement.

• Cons:

  • It is only first-order accurate (error is proportional to $h$); hence, for a given step size $h$, it may not be very accurate.
  • It may require very small step sizes to achieve acceptable accuracy, increasing computational cost.

---

Example 1

So let’s say we have this equation and it’s derivative :

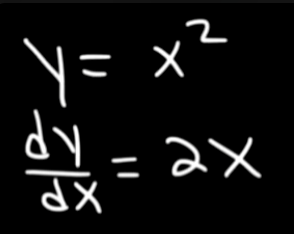
Note that this is an explicit equation, so we need to find out the derivative ourselves.

We need to approximate the value of $y$ when $x=1.5$.

So, since this method requires very small step sizes for good accuracy, let’s set :

$h=0.1$

Another of finding the step size would be:

First, let $x=1.5=b$ and the starting point $x=1=a$ (since we take $x,y=(1,1)$) as the initial points

$h=\frac{b-a}{n}$

So if we took $n=4$,

then :

$h=\frac{0.5}{4}=0.125$

which results in a more precise step size, so we might get a more precise value if we use this step size.

But for consistency with the example in the video, we will use $h=0.1$.

So here :

$f(x)=x^2$

$f^{\prime }(x)=2x$

So since our equation depends on $x$, so we will use the equation :

$y_{n+1}=y_n+h{f}^{\prime }(x_n)$

So let’s create a table first :

n	$x_n$	$y_n$	Actual value

And start off with the initial point P(1,1), where $x_n=1$ and $y_n=1$ and $n=0$.

n	$x_n$	$y_n$	Actual value
0	1	1

Here $x_n=x_n+h$

So the value of $x_n$ will increase by the step size.

Now we use the equation :

$y_{n+1}=y_n+h{f}^{\prime }(x)$

to predict the values for the next iterations.

We will continue till $n=4$, that way we get the value till $y_5$ or $n=5$ iterations.

So, for $n=0$,

$y_1=y_0+0.1\times (2\times 1)$

$⟹y_{1.1}=1+0.2=1.2$

n	$x_n$	$y_n$	Actual value
0	1	1
1	1.1	1.2

Next, for $n=1$

$y_2=y_1+0.1\times (2\times 1.1)$

$y_2=1.2+0.1\times 2.2=1.2+0.22$

$y_2=1.42$

n	$x_n$	$y_n$	Actual value
0	1	1
1	1.1	1.2
2	1.2	1.42
3	1.3
4	1.4
5	1.5

Next, for $n=2$

$y_3=y_2+0.1\times (2\times 1.2)$

$y_4=1.42+0.24$

$y_3=1.66$

n	$x_n$	$y_n$	Actual value
0	1	1
1	1.1	1.2
2	1.2	1.42
3	1.3	1.66
4	1.4
5	1.5

Next, for $n=3$

$y_4=y_3+0.1\times (2\times 1.3)$

$⟹y_4=1.66+0.1\times (2\times 1.3)$

$⟹y_4=1.66+0.26$

$⟹y_4=1.92$

n	$x_n$	$y_n$	Actual value
0	1	1
1	1.1	1.2
2	1.2	1.42
3	1.3	1.66
4	1.4	1.92
5	1.5

Now, for $n=4$

$y_5=y_4+0.1\times (2\times 1.4)$

$y_5=1.92+0.1\times (2\times 1.4)$

$y_5=1.92+0.28=2.2$

n	$x_n$	$y_n$	Actual value
0	1	1
1	1.1	1.2
2	1.2	1.42
3	1.3	1.66
4	1.4	1.92
5	1.5	2.2

Now, time to find out the actual values per value of $x_n$

So we will use the original equation, $y=x^2$ .

So, $y(1)=1$

n	$x_n$	$y_n$	Actual value
0	1	1	1
1	1.1	1.2
2	1.2	1.42
3	1.3	1.66
4	1.4	1.92
5	1.5	1.1

$y(1.1)=1.21$

$y(1.2)=1.44$

$y(1.3)=1.69$

$y(1.4)=1.96$

$y(1.5)=2.25$

n	$x_n$	$y_n$	Actual value
0	1	1	1
1	1.1	1.2	1.21
2	1.2	1.42	1.44
3	1.3	1.66	1.69
4	1.4	1.92	1.96
5	1.5	2.2	2.25

So, we get our final approximation of $y(1.5)$ as $2.2$, which is real close to the actual value, $2.25$

What is the “actual value” btw?

In the cases of ODEs and not explicit equations, it’s used to update the value of $y_n$, but it’s not considered the actual approximation itself.

So our final answer will be $2.2$.

---

Example 2

https://www.youtube.com/watch?v=U8-4HLKtmDM&list=PLU6SqdYcYsfLrTna7UuaVfGZYkNo0cpVC&index=10

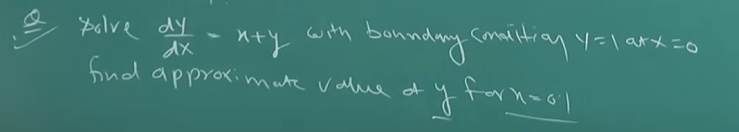
Note that this is NOT an explicit equation, but rather an ODE, so we don’t need to find out the derivative ourselves.

In this case, the formula becomes :

$y_{n+1}=y_n+hf(x,y)$

Since our given $f(x,y)$ is already the derivative itself.

So we are given a starting condition as :

$y=1$ and $x=0$ and we need to find $y$ at $x=0.1$

Let’s compute till $n=5$.

So the step size will be :

$h=\frac{0.1-0}{5}=0.02$

So using that we construct our table:

n	$x_n$	$y_n$	$f(x,y)$
0	0	1	1
1	0.02	1.02	1.04
2	0.04	1.04	1.08
3	0.06	1.06	1.12
4	0.08	1.08	1.16
5	0.1	1.11	1.21

I got the values early on since I made a program to calculate all this

[[0, 0, 1, 1]]
[[1, 0.02, 1.0204, 1.0404]]
[[2, 0.04, 1.0416079999999999, 1.081608]]
[[3, 0.06, 1.0636401599999998, 1.1236401599999999]]
[[4, 0.08, 1.0865129632, 1.1665129632]]
[[5, 0.1, 1.110243222464, 1.210243222464]]
The value of y at x = 0.1 is: 1.110243222464 

However I will do some of them by hand to clear up any confusion.

So for $n=0$

$y_1=y_0+hf(x_0,y_0)$

$⟹y_1=1+0.02\times (0+1)$

$⟹y_1=1.02$

Similarly for $n=1$

$y_2=1.02+0.02\times (0.02+1.02)$

$⟹y_{@}=1.02+0.00208$

$⟹y_2\approx 1.04$

And so on… I assume you can do the rest of the calculations by yourself.

So the final approximation of $y(0.1)$ is $1.1102$. And the value in the video was obtained as $1.108$ is due to precision differences.

---

2. Runge-Kutta Method (or Euler’s Modified Method)

This method is used for 2nd order differential equations.

This is based upon Euler’s method by modifying it.

$y_{n+1}^{\ast }=y_n+hf(x_n,y_n)$

(obtained by using Euler’s method)

then, we use this to get :

$y_{n+1}=y_n+\frac{h}{2}[f(x_n,y_n)+f(x_{n+1},y_{n+1}^{\ast })]$

Example 1:

Let’s say we have :

$\frac{dy}{dx}=x^2+y$

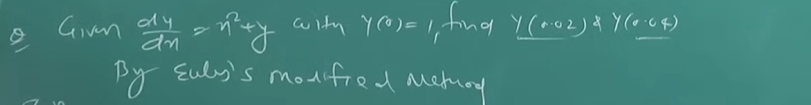
Another ODE, not an explicit equation.

We are given the starting conditions as $y(0)=1$ which means :

$x_0=0;y_0=1$

And we are asked to find the value of $y$ at $x=0.02$ and $x=0.04$

So if we continue till $n=5$, then the step size, $h$ will can be taken for simplicity purposes as :

$h=0.02$

Since we will be finding for two $x$ values and the difference between then is $0.02$ so for simplicity purposes we can take $0.02$

Or for better accuracy we can :

$h=\frac{0.02}{5}=0.004$

Let’s find out which step size leads to more precise answer :

So, at $n=0andh=0.02$

We will have our table as :

n	$x_n$	$y_n$	$f(x_n,y_n)$
0	0	1	1
1	0.02
2	0.04
3	0.06
4	0.08
5	0.10

We see that we can get the required $x_n$ values at a lesser number of iterations if we use $h=0.004$

$y_1^{\ast }=y_0+0.02\times (0^2+1)$

$⟹y_1^{\ast }=1+0.02=1.02$

And $y_1=1+\frac{0.02}{2}\times [(0^2+1)+(0.02^2+1.02)]$

$⟹y_1=1+(0.01\times 2.0204)$

$⟹y_1=1+0.0020204=1.020204$

Now at $n=1$

$y_2^{\ast }=y_1+0.02\times (0.02^2+1.020204)$

$⟹y_2^{\ast }=1.020204+(0.02\times 1.020604)$

$⟹y_2^{\ast }=1.020204+0.02041208$

$⟹y_2^{\ast }=1.04061608$

Now,

$y_2=1.020204+0.02\times [(0.02^2+1.020204)+(0.04^2+1.04061608)]$

$y_2=1.020204+\frac{0.02}{2}\times [0.02041208+1.04221608]$

$y_2=1.020204+0.01\times 1.06262816$

$⟹y_2=1.020204+0.0106262816$

$⟹y_2=1.030830282$

n	$x_n$	$y_n$	$f(x_n,y_n)$
0	0	1	1
1	0.02	1.020204	0.0020204
2	0.04	1.030830282	0.0106262816
3	0.06
4	0.08
5	0.10

So we have our as $y(0.02)=1.020204$ and $y(0.04)=1.030830282$

---