Index
- Basic Terminologies
- Chomsky Hierarchy of languages
- Deterministic Finite Automata (DFA)
- Non-deterministic Finite Automata
- Finite Automata with outputs.
- Conversion of NFA to DFA
- Regular Expressions
- Identities of Regular expressions
- Conversion of NFA to Regular Expression
- Conversion of Regular expression to Finite Automata
- Pumping Lemma for Regular Languages.
- Regular Grammar
- Derivations from a Grammar
Basic Terminologies
- Symbol : Any alphanumeric stuff : “a, b, c, 0, 1, 2, 3”… and so on.
- Alphabet : , denotes a collection of symbols. For example or or
- String : “A sequence of symbols”. For example: “a,b,0,1,aa,bb,ab,01”
- Language: A set of strings. For example
Let L1 be a set of strings of length 2
Therefore
L2 = Set of strings of length 3
This can also be expressed as powers of .
For first case, it will be L1 =
For second case, it will be L2 =
Finite Automata
There’s two types of Finite Automata
- Finite Automata without Output:
- Deterministic Finite Automata (DFA)
- Non-Deterministic Finite Automata (NFA)
- Finite Automata with Output:
- Moore Machine
- Mealy Machine
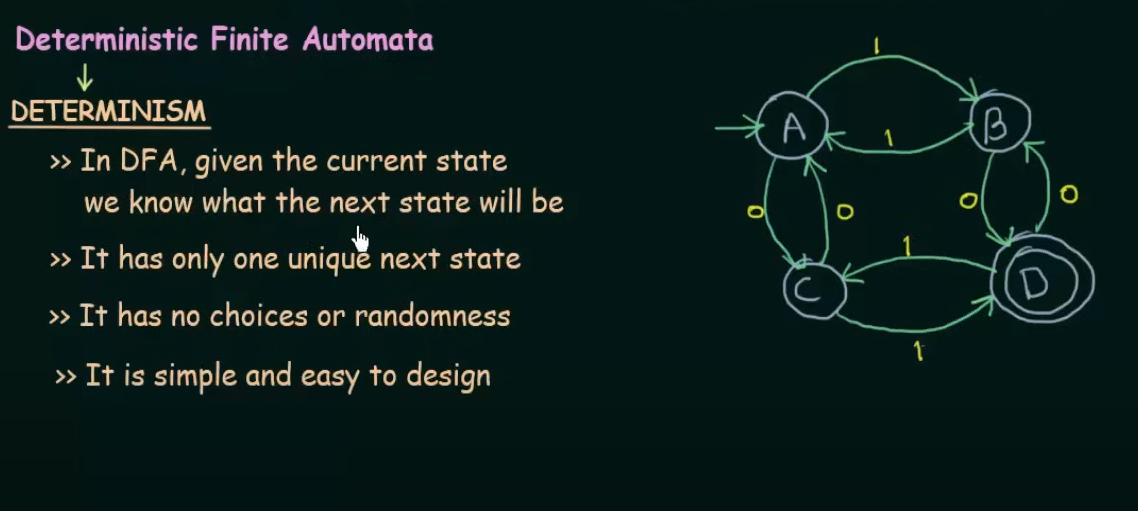
Deterministic Finite Automata (DFA)
- It is the simplest model of computation
- It has a very limited memory.
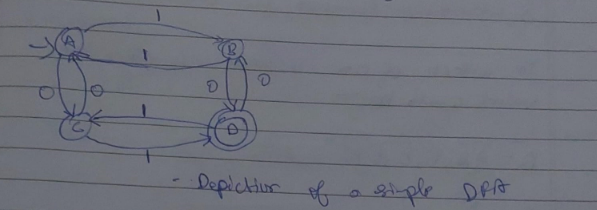
Here A,B,C,D are the states. The edges having “0” or “1” are the inputs and also the transition states which determine which state will the DFA shift to.
The incoming arrow at state A indicates that A is the starting state.
The double circle in state D indicates that it is the final state of the DFA.
Every DFA/NFA can be defined using these 5 tuples
(Q, , , F, )
 Symbol Pronunciation
Symbol Pronunciation
= sigma (not the brainrot sigma kid) = q “not” = delta
Example

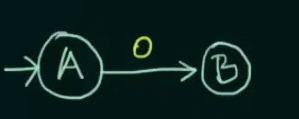
Start from initial state A. Since we can only have input strings which start with 0, we send it to a final state B. Now in case B receives any more inputs, those will be looped at B.
Now we need to take care of the case of input strings starting with 1. Therefore we design another state C where those strings are sent and subsequent inputs in C, stay at C.
This state C is also known as the “dead state” where unwanted strings go to in DFA.
More DFA example videos:
https://www.youtube.com/watch?v=40i4PKpM0cI&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=4 https://www.youtube.com/watch?v=2KindKcLjos&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=5 https://www.youtube.com/watch?v=_2cKtLkdwnc&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=6
Non-deterministic Finite Automata

The main difference between DFA and NFA is that in DFA all the states are ==pre-determined== and there is only one unique next state, however in NFA there could be, given the current state multiple next states and the next state may be chosen at random and all the next states could be chosen in parallel.

Here, instead of sending the input strings which start with 1 to a dead state C, it was looped into A itself.
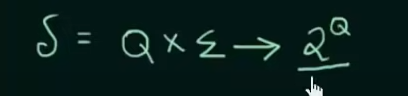
Examples
 Let’s test this using a test string “100”
Let’s test this using a test string “100”
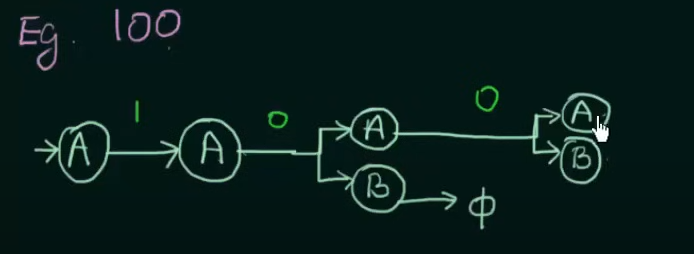
and another test string “01”
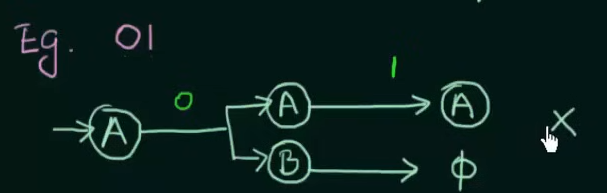

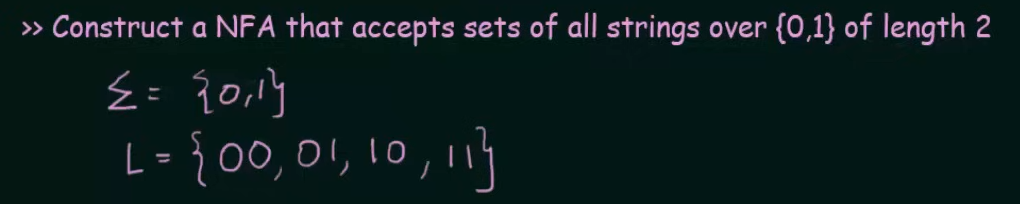
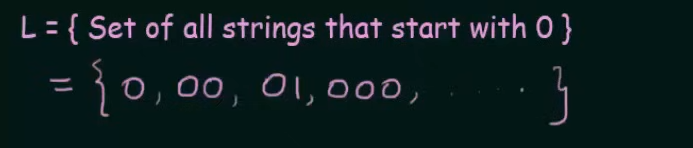 Let’s create an NFA for this set
Let’s create an NFA for this set
We start with our initial state A and another state B
We declare B as final state and for any subsequent inputs to B, we loop them into B itself
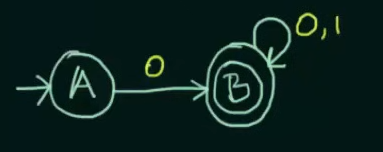
Now we could have looped inputs of 1 into A itself, or sent it to a final state in case of a DFA, but in this case of an NFA, this NFA is complete.
Example test strings
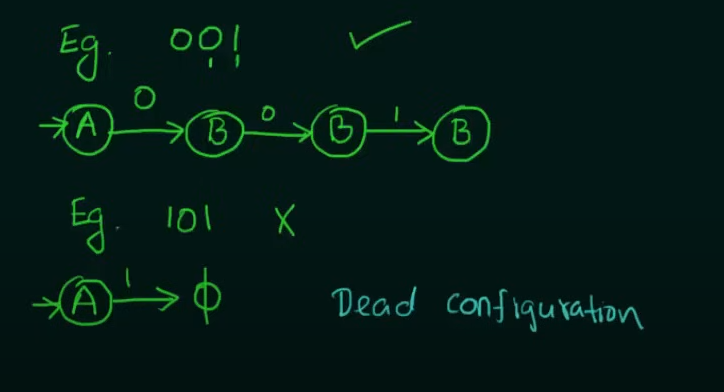
So we need to make two states whose combined inputs will result in a string of length 2 and a final state to hold the strings.
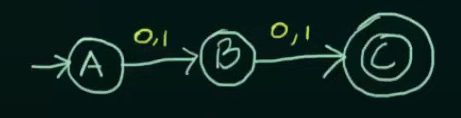
Note that we want our NFA to be restricted to the values of set L and thus we didn’t make any changes to final state C.
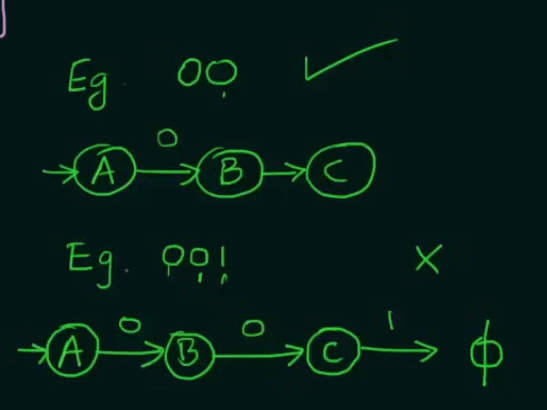
All example videos on NFA:
https://www.youtube.com/watch?v=4bjqVsoy6bA&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=12 https://www.youtube.com/watch?v=Bcen1W_uFEU&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=13 https://www.youtube.com/watch?v=—CSVsFIDng&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=15
Conversion of NFA to DFA

Example.
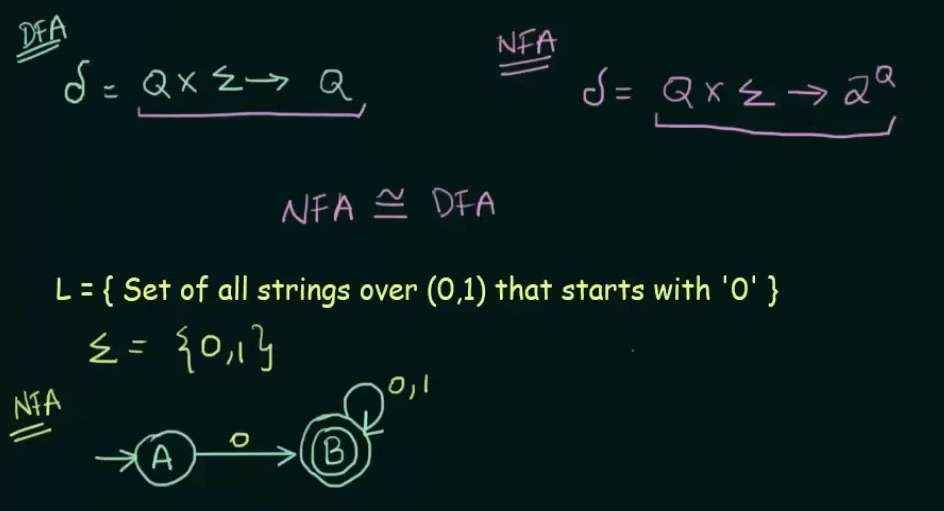
Given NFA here.
Step 1. Make the state transition table for the NFA.
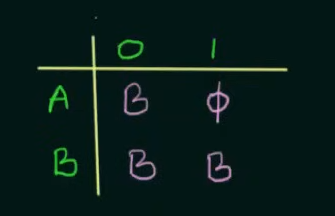
Here as we can see, on input 0, A goes to B and on input 1, A goes to (NULL) On input 0, B loops back to itself and on getting input 1, B goes to (NULL)
Step 2. Make the state transition table for the resultant DFA from the state transition table of the NFA.

Since we cannot leave unwanted strings to loop in any other state than a dead state in DFA, we put a new state C in place of .
And since we created a new state C, we need to define the transitions on C as well, which loops to itself despite any input to state C.
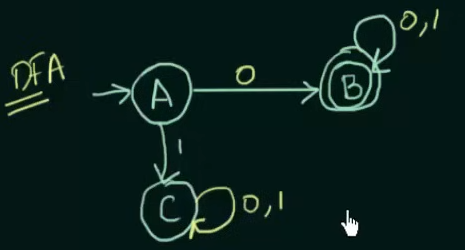
Thus the new resultant DFA.
Example 2. (Important)
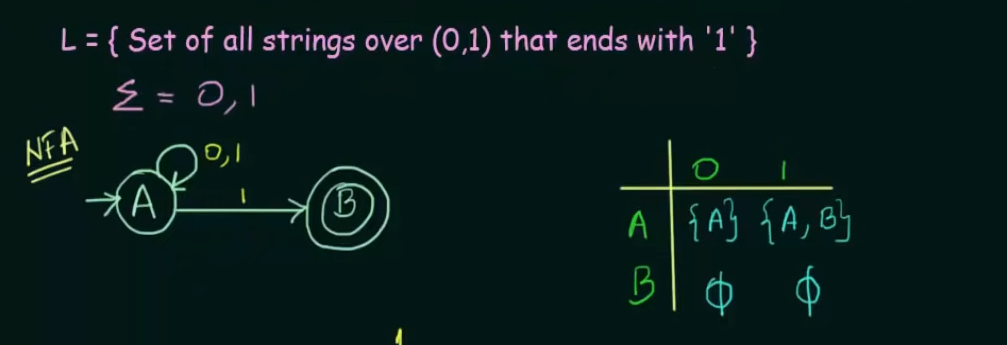
Here’s our given NFA and it’s transition state table. Note that on an input of 1, state A loops to itself and also goes to final state B, to represent that we created a new state which represents states .
In case of a DFA since there is ==only one unique next state== we need to represent using a new state AB.
And we also need to define the state transitions of AB.
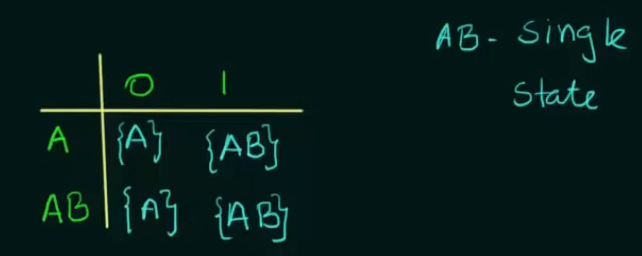
This method of creating new states which contains more than one state is called “Subset creation method”.
Thus the resultant DFA will be:
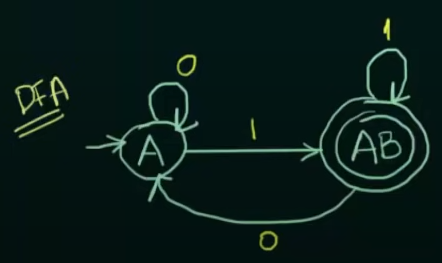
More example videos :
https://www.youtube.com/watch?v=i-fk9o46oVY&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=17
https://www.youtube.com/watch?v=dY1bCC6syLI&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=18
https://www.youtube.com/watch?v=dY1bCC6syLI&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=18
https://www.youtube.com/watch?v=Y92dtMnarAU&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=19
Minimization of DFA
Minimization of DFA is required to obtain the minimal version of any DFA which consists of the minimum number of states possible.

Let’s understand this practically using examples.
Example 1.
Given a DFA and it’s state transition table.
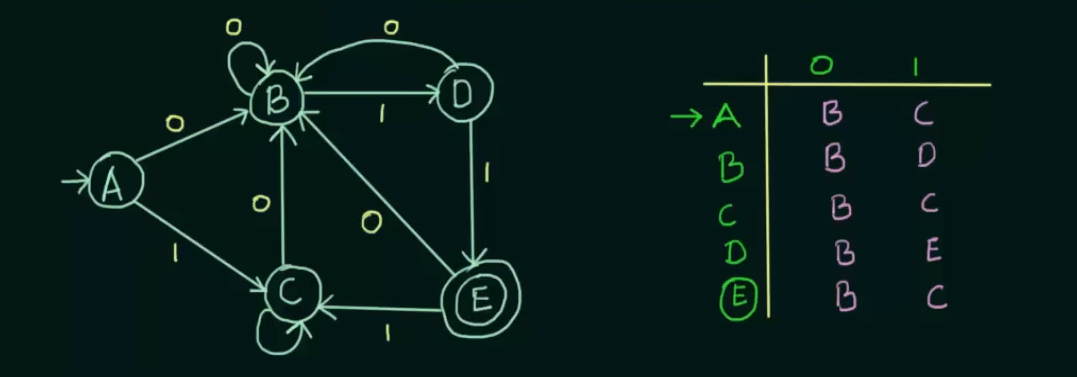
Step 1. Write the zero equivalence as two separate sets : {Set of non-final states} {Set of final states}
0 equivalence =
Step 2. Write 1 equivalence.
Here we see that in the first set, there are 4 states. Now we need to see if those states are 1 equivalent to each other. How we do that is we take pairs of the sets, then check if the next states of the pairs are equal to each other . If so then the pair is 1 equivalent to each other.
We get to see that for input 0, both A and B go to state B and for input 1, we see that A goes to state C and B goes to state D.
Thus we need to check if C and D are 1 equivalent to each other or not.
We see that both C and D go to state B on input 0 and on input 1, C loops to itself and D goes to state E.
Now we also see that A and C share the same next states for both inputs.
Thus C and D are not 1-equivalent to each other.
Therefore
1 equivalence =
Step 3: Check for 2-equivalence using the same method
Use the row of 1-equivalence
We will only focus on the set of
We know that on input 0, A and B go to the same states, but on input 1, A goes to state C and B goes to state D.
Check if C and D are in the same set or not. [False]. Thus A and B are not 2-equivalent to each other.
Thus,
2 equivalence =
Now we see that for any further equivalences, the result is the same, so we can stop the process here.
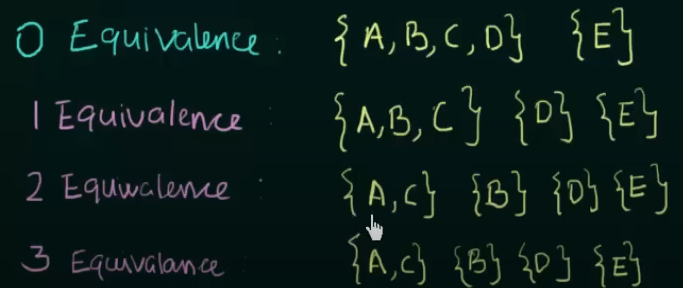
Now using this equivalence and the existing transition state table, we get the new minimized DFA
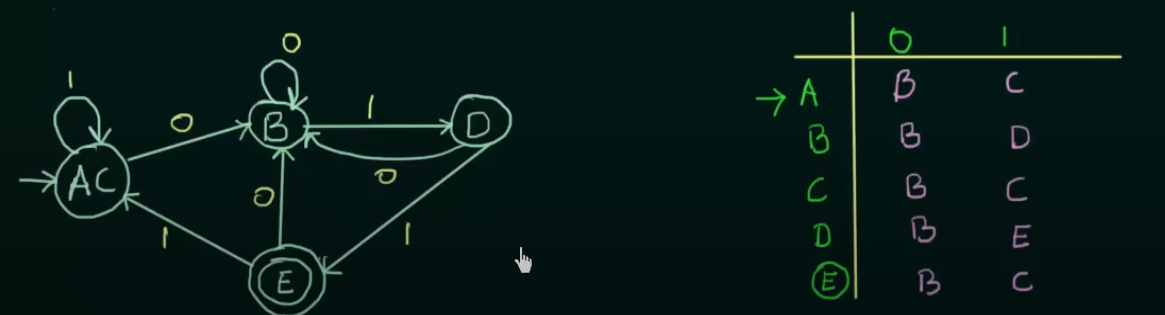
Where AC is treated as a single new state.
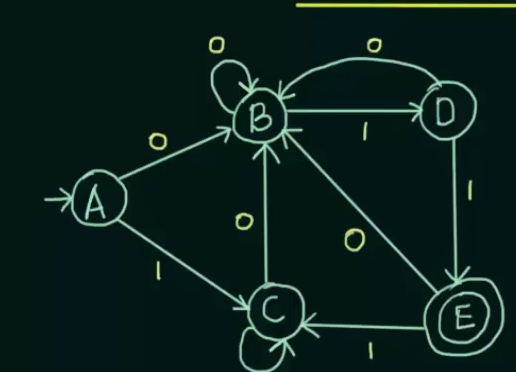
Therefore, DFA before minimization
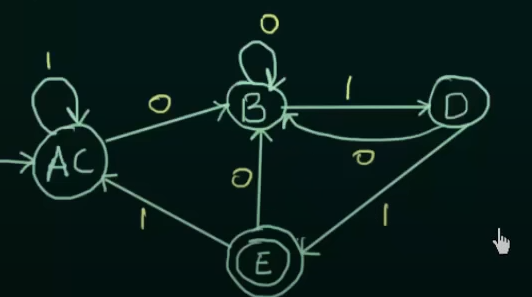
And DFA after minimization
More examples on the DFA minimization
https://www.youtube.com/watch?v=0XaGAkY09Wc&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=21 https://www.youtube.com/watch?v=ex9sPLq5CRg&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=22 https://www.youtube.com/watch?v=DV8cZp-2VmM&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=23 https://www.youtube.com/watch?v=kYMqDgB2GbU&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=24
Finite Automata with outputs.
Till now the automata we dealt with produced no outputs.
Now we will be dealing with automata with outputs.

Don’t focus on the symbol descriptions too much, it’s just filler theory.
Example

The main difference between Mealy Machine and Moore Machine is that
Mealy Machines produce outputs during the transition phase (When A goes to A or B or wherever)
Moore Machines produce outputs within the state itself (When A or B or any other state is reached)
Construction of Mealy Machine

Now we know that outputs in Mealy machines are produced during the transition phase.
There for any strings like this :

will result in a Mealy Machine like this :
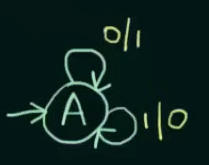
The format of “0/1” is : input/output, saying that the first half indicates the input of the state and the second indicates the output.

Here = the set of inputs and = the set of outputs
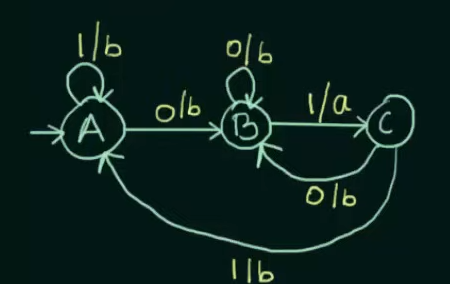
This will be resultant Mealy Machine.
Here since we want the sequence “01” only, hence we send the input of 0 from C to B and the input of 1 from C to A.
And the transition phase from B to C of 1, resulting in the total sequence of “01”, will output the string a, the rest of the inputs will output the string b, but are looped into themselves or sent to other states.
Example

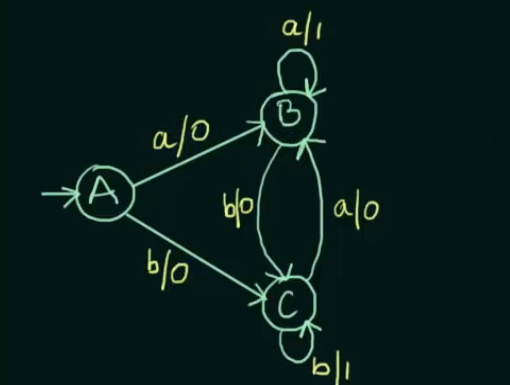
This will be the resulting Mealy Machine
More examples
https://www.youtube.com/watch?v=s-Ul9dIS9AE&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=29 https://www.youtube.com/watch?v=fkdufhcBraw&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=30
Construction of Moore Machine

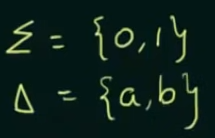
Step 1. Construct a DFA for a binary string that will end with 01.
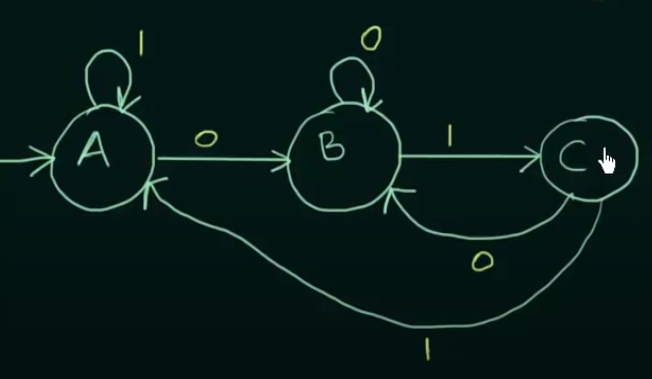
Now just add the outputs to the states
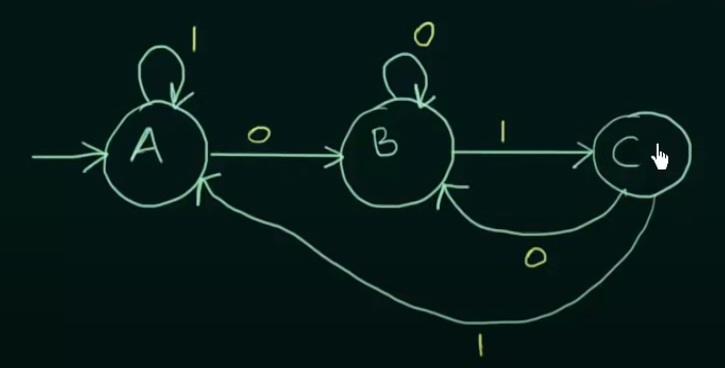
More example videos :
https://www.youtube.com/watch?v=BQPSt8dRX1Q&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=32 https://www.youtube.com/watch?v=UKTzwXSJiIk&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=33
Conversion of Moore to Mealy machine
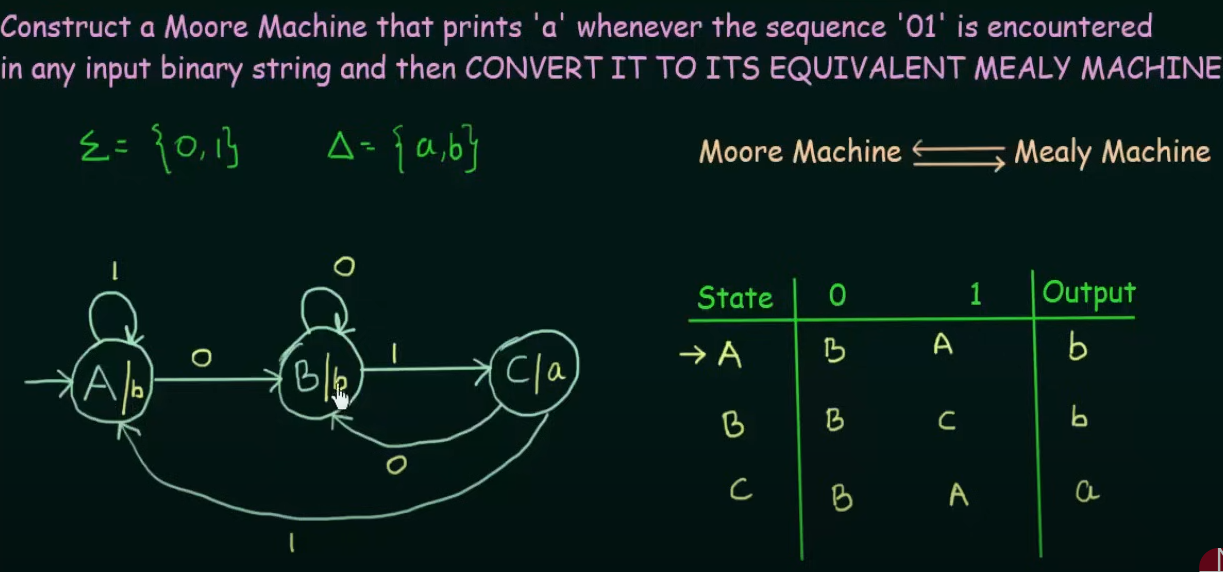
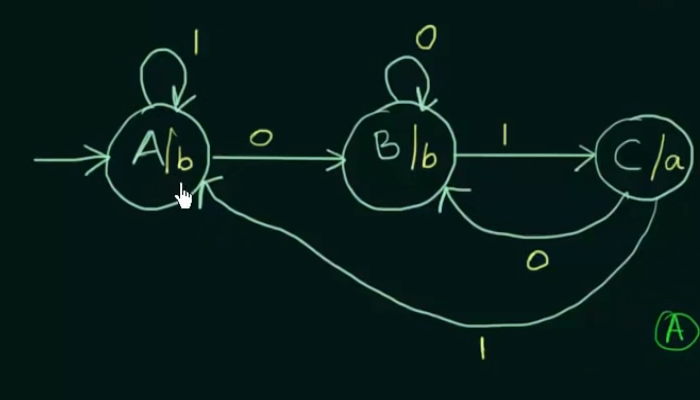
Here, we have been given a Moore Machine.
To convert to a Mealy machine, we have to put the same output of the state to it’s incoming edge.
Therefore the resulting Mealy Machine will be :
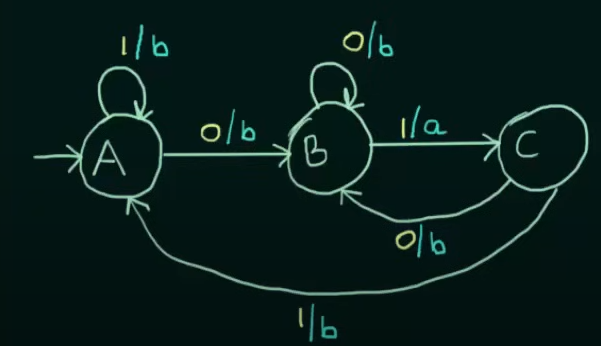
And we need to change the state transition table accordingly by writing the outputs besides the states and removing the output column :

More example videos :
https://www.youtube.com/watch?v=lqvVtBdazvg&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=35 https://www.youtube.com/watch?v=GHStZkC080k&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=36
Conversion of Mealy Machine to Moore Machine

Thus set of inputs , = {a, b} and set of outputs = {1,0}
Now since states B and C output two different values, they will be separated into states and .
And the output on the states will be the same the outputs on the edges incoming to them.
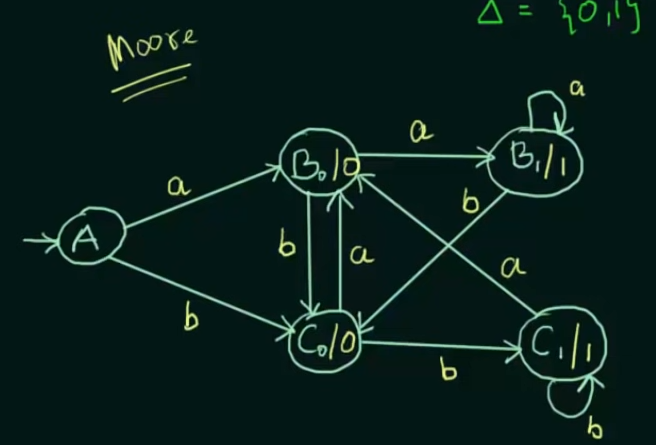
Now state A didn’t have to be separated since there are no incoming outputs on A.
Another example video :
https://www.youtube.com/watch?v=t48LqMDqNrA&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=39
Regular Languages

Regular Expressions


Important operations to remember in Regular Expressions.
- Union : The union of any two RE is denoted by
- Concatenation : The concatenation of any two RE is denoted by
- Iteration/Closure: The iteration of any RE is denoted by . For example :
= { ^, a, aa, aaaa}… where ^ is called the empty symbol. The empty symbol’s presence is mandatory for such an RE to be considered a closure.
Examples

Any comma in the set is denoted by Union (or), but if it has the empty symbol as in example 2, it is denoted by concatenation(and).
Identities of Regular expressions

https://www.youtube.com/watch?v=yp4pYgXfYD8&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=47
Arden’s Theorem

Proof in case someone wants to memorize this

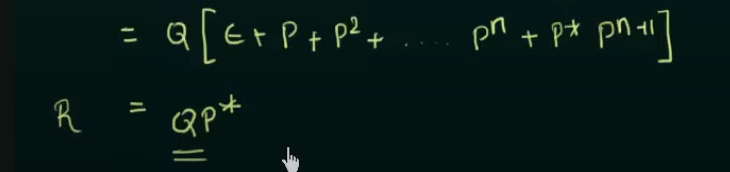
https://www.youtube.com/watch?v=Idl_0mPzZjE&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=48
Example video
https://www.youtube.com/watch?v=TkqcPh0BFUw&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=49
Designing of Regular Expressions

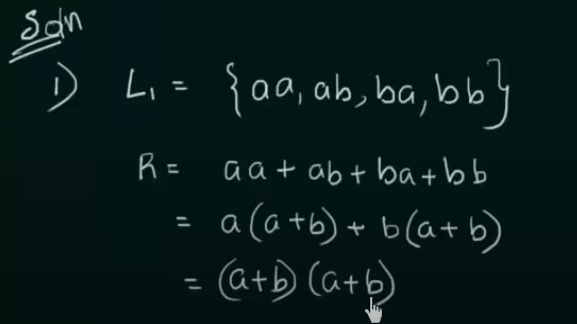
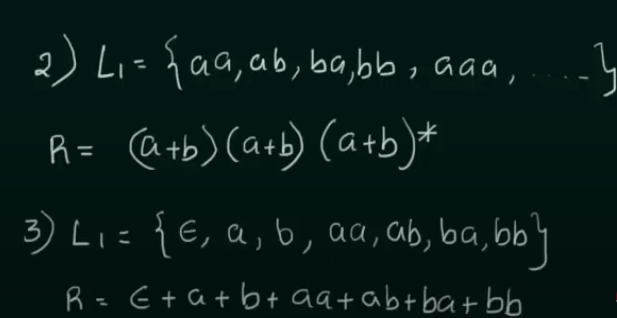
https://www.youtube.com/watch?v=FOhEmW_nMRs&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=50
Conversion of NFA to Regular Expression
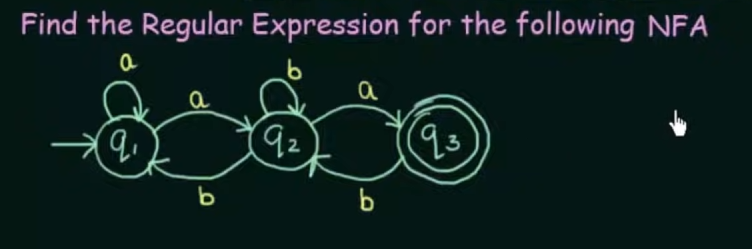
Step 1. Create equations of each state which includes it’s incoming state transitions
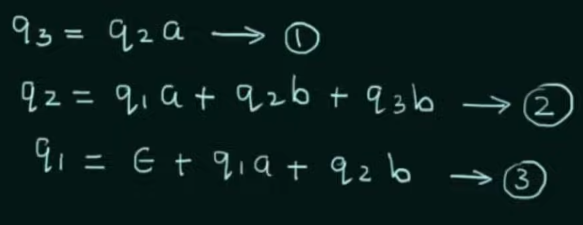
Solve the equations to get an RE in terms of the final state.
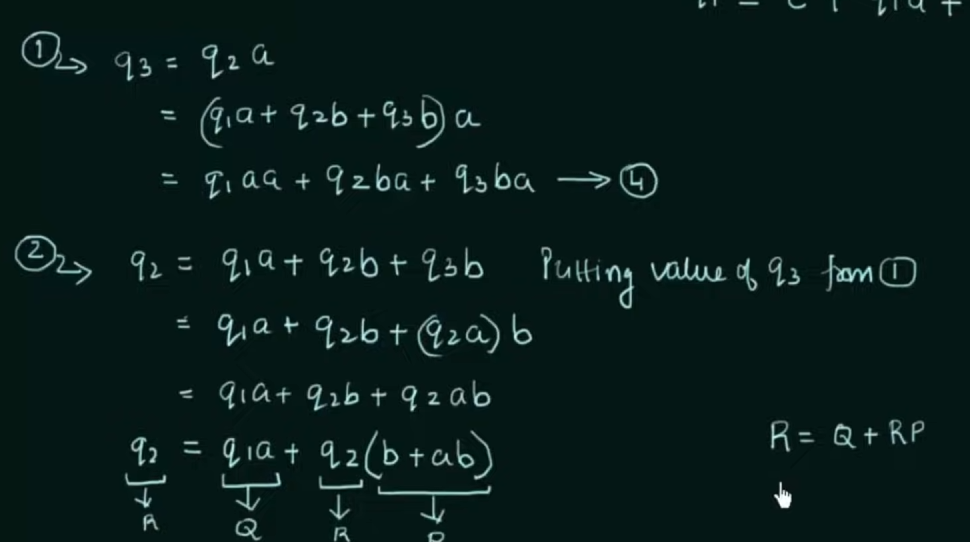
Thus, by Arden’s Theorem:
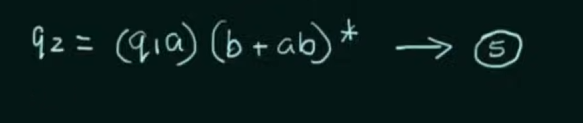
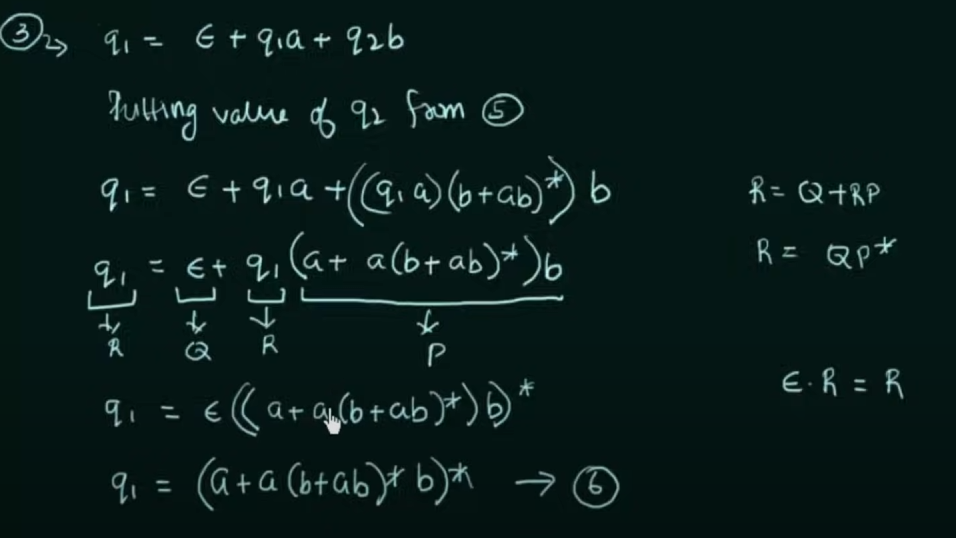
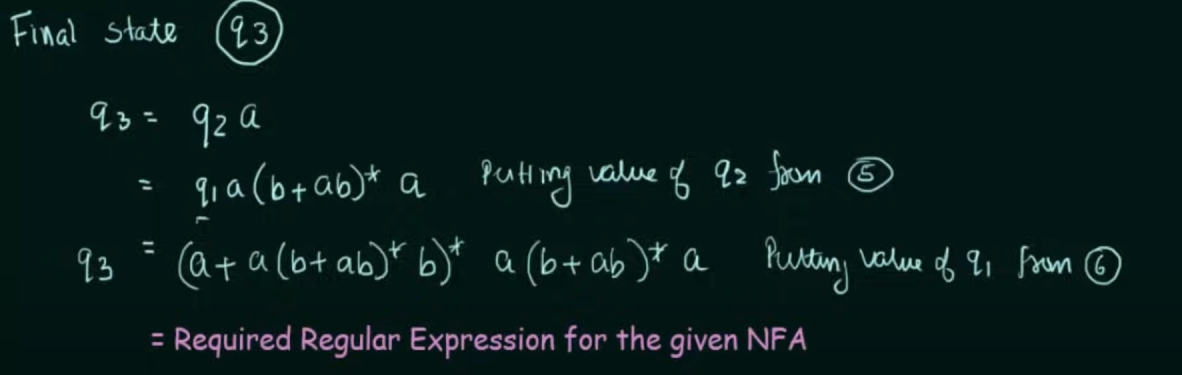
Conversion of DFA to Regular Expression
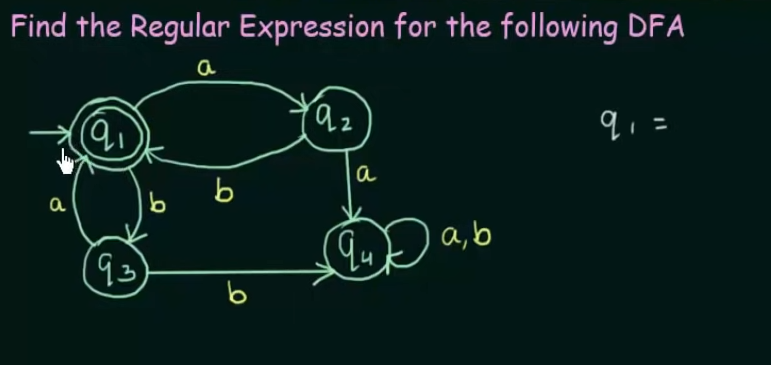

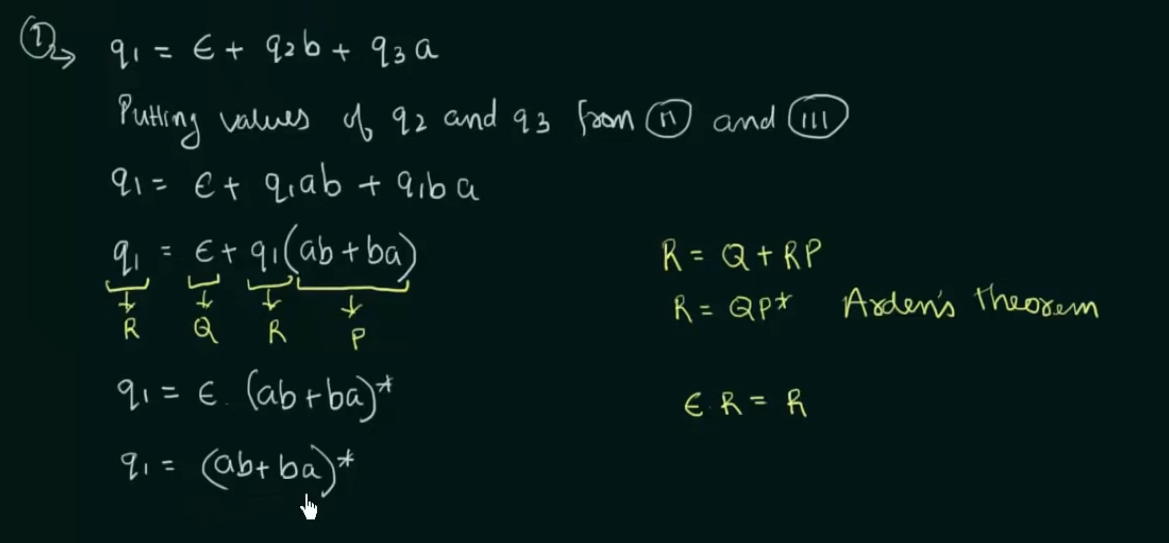
Example 2: When DFA has multiple final states

Find RE in terms of both the final states then perform a Union of the two
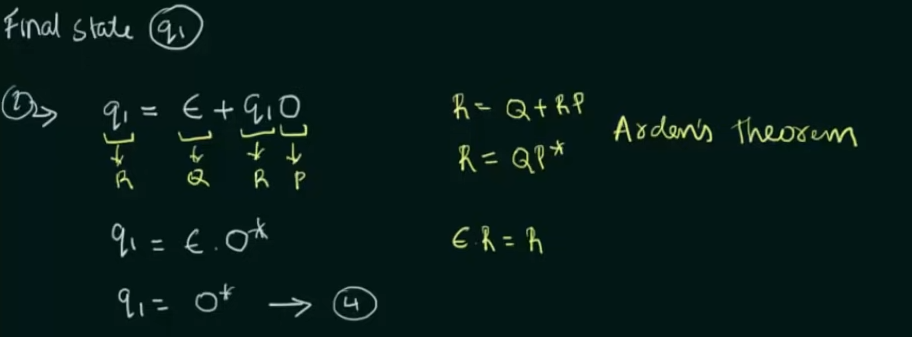

Conversion of Regular expression to Finite Automata

Union : both inputs can go to the same state. Concatenation: Will need two states of one input each Closure: Will loop into that state itself.
Example
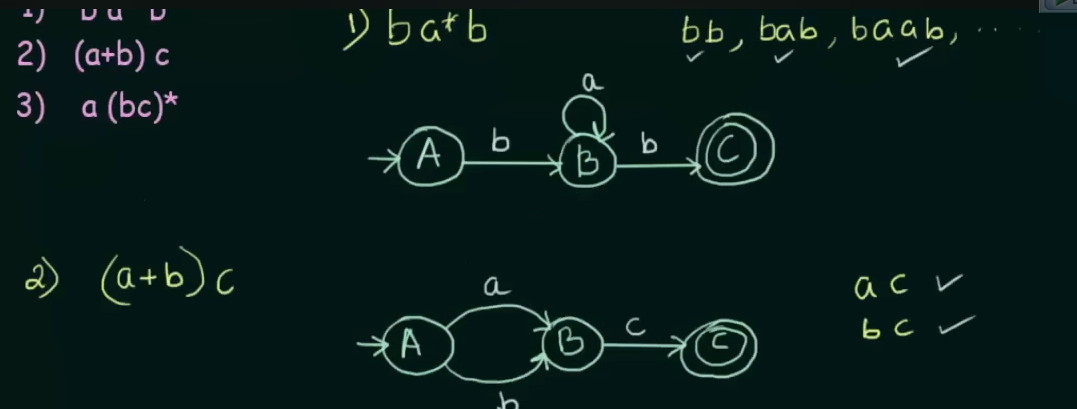
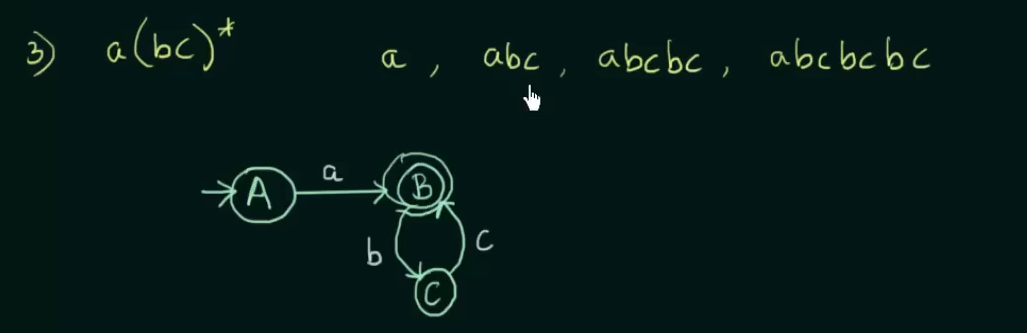

All example videos on this topic :
https://www.youtube.com/watch?v=62JAy4oH6lU&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=55 https://www.youtube.com/watch?v=RsSQPwUIR8U&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=56 https://www.youtube.com/watch?v=zSHS_7omxRY&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=57
Equivalence of two finite automata

Basically what we need to do is to see that for any pair of states, ==the pair of states both should either be intermediate states or final states==.
And if ==If the initial state of one automata is a final state, it should be the same for the other automata==.

Here FS stands for Final State and IS stands for intermediate state.
Example

Here we can see that the second point is already satisified.
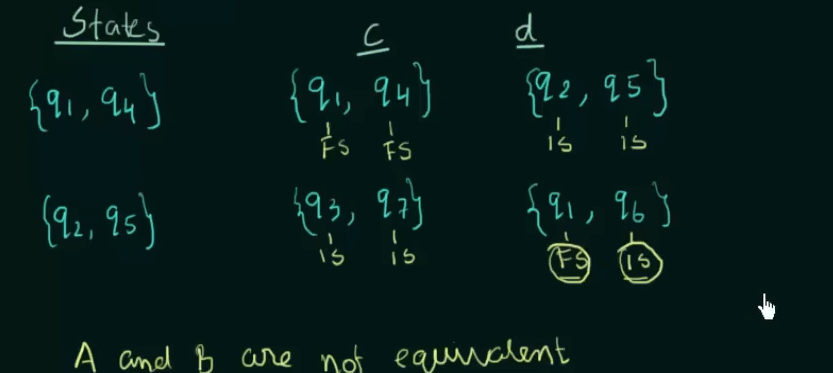
Here we could see that on input d, state q2 went to state q1 which is a final state and state q5 went to state q6 which is a intermediate state. This goes against the rule that for any two automata, any selected pair of states should be of the same kind.
Thus the automata A and B are not equivalent.
Pumping Lemma for Regular Languages.

**
Example
https://www.youtube.com/watch?v=Ty9tpikilAo&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=61

Let us assume that A is regular
Then it must have some pumping length P
Let P = 7
Therefore A = (we can also take the string variable as S, but A is preferred to maintain consistency)
Now we can break down A (or S) into three parts such that
Therefore let S = aaaaaaaabbbbbbb (contains 7 a and 7 b)
Since this entire string can be broken down into three parts , we can check for the satisfiability of the first condition
Thus we get three cases

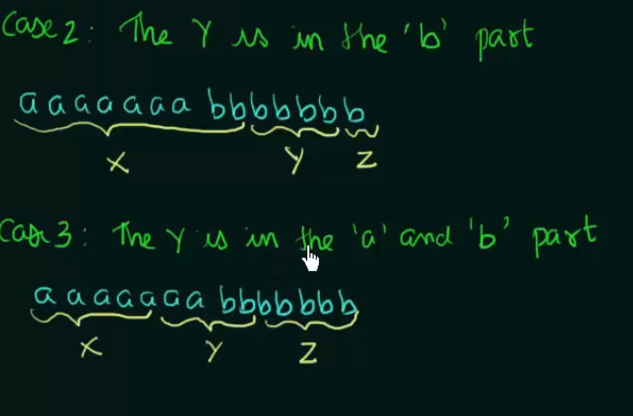
Now we need to show that none of the three conditions can be satisfied at the same time (could be none at all, or 2 satisfied 1 unsatisfied or 1 unsatisfied 2 satisfied but not 3 satisfied at the same time).
So, for the first condition, let i = 2.
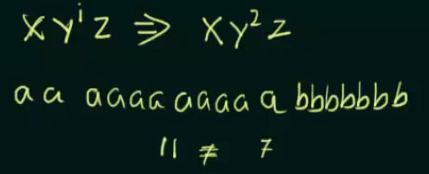
so, according to case 1, and the value of i, we need to write the part of y twice.
and we find that the total number of strings is greater than that of the pumping length P.
Thus case 1 does not satisfy the first condition.
Similarly :
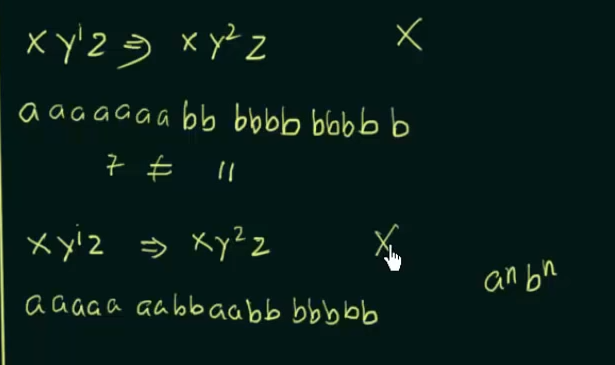
Since the first condition itself couldn’t be satisfied, we don’t need to check the remaining two conditions. Hence, the language is NOT regular.
Another example video
https://www.youtube.com/watch?v=kZzH8E-s-9o&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=62
Regular Grammar
https://www.youtube.com/watch?v=WgEsPTAL55Q&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=63
Chomsky Hierarchy of languages




Derivations from a Grammar
https://www.youtube.com/watch?v=ejXgLRSIxsA&list=PLBlnK6fEyqRgp46KUv4ZY69yXmpwKOIev&index=64