Semester 3 Recap

What is a Graph?

A graph is a mathematical structure containing 2 sets V and E where V represents a non-empty set of vertices and E represents a non-empty set of edges.

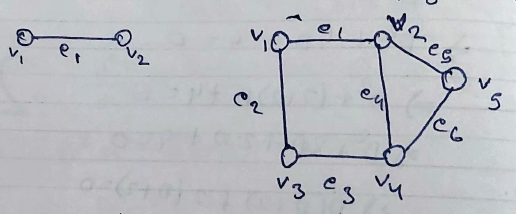
Basic Terminology

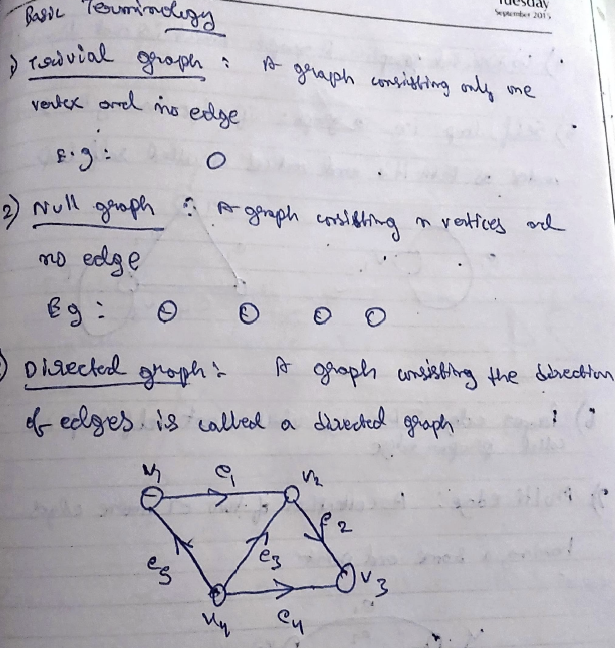
Trivial Graph : A graph containing only one vertex no edge.
Null Graph: A graph containing n vertices and no edge.
Directed Graph: A graph consisting the direction of edges is called a directed graph.
Undirected Graph: A graph which is not directed.
Self loop in a graph: If edge having the same vertex as both it’s end vertices is called a self loop.
Proper edge: An edge which is not self loop is called proper edge.
Multi edge: A collection of two or more vertices having a same end point.

Types of Graph

Complete Graph: A simple connected graph is said to be complete if each vertex links to every other vertex.
Regular Graph: A graph G is said to be regular if every vertex has the same degree. If the degree of each vertex of graph G is K, then it is called K-regular graph.
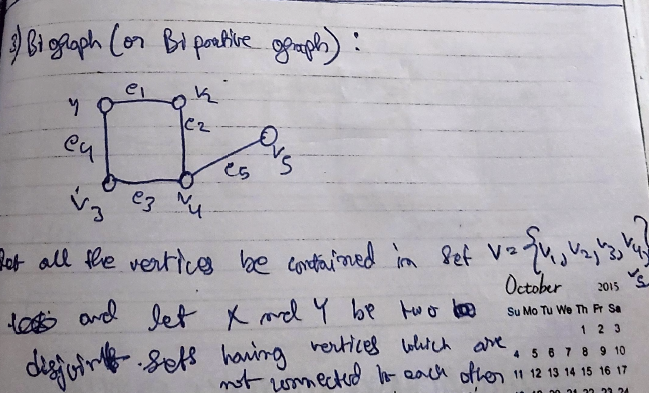
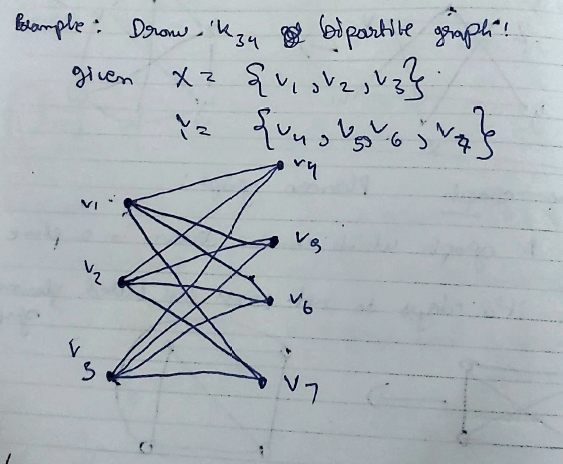
Bi-graph (or Bipartite Graph): Let all the vertices contained in set

$V = {v 1, v 2, v 3, v 4, v 5}$ and let X and Y be two =disjoint sets= having vertices which are not connected to each other :

$X = {v_{1}, v_{4}}$ and

$Y = {v_{3}, v_{2}, v_{5}}$
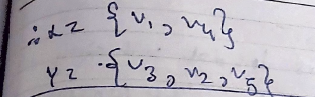
Complete Bi-partite graph: If every vertex in X is disjoin with every vertex in Y, then the graph is called a complete Bi-partite graph.
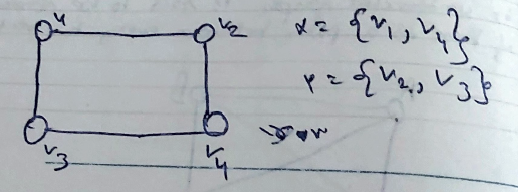
Subgraph : Let there be a graph G(V, E), V and E being the two sets for it’s vertices and edges. Let V’ and E’ be the subsets of V and E respectively. Thus G(V’, E”) is a graph and subgraph of G(V, E).

Complement of a graph.

The complement of a graph is basically the :

connection of previously unconnected vertices

and

removal of the connection of currently connected vertices

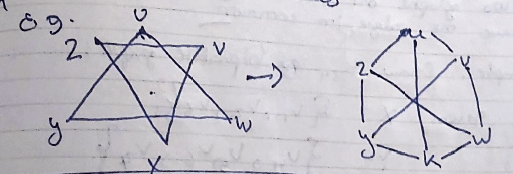
Planar Graph

A graph which can be drawn in a plane so that it’s edges do not cross are called planar graphs.

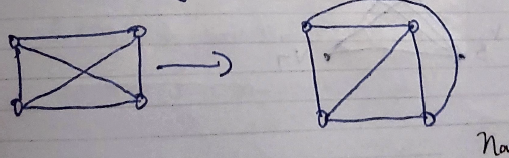
Self loops or parallel edges may be allowed here.

Di-graph (or Directed Graph)

It is a type of graph where each edge has a direction.

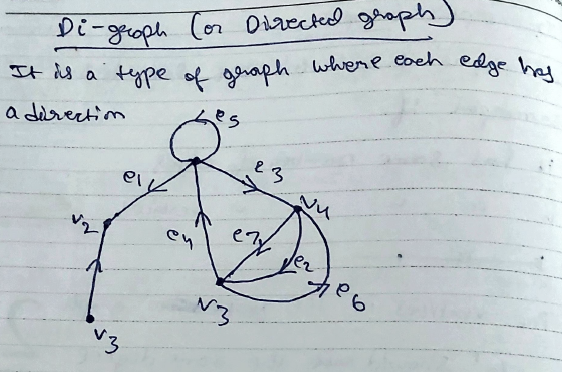
The starting vertex is called the initial vertex.

The vertex which has no incoming edges but only outgoing edges is called a source.

The vertex which has only incoming edges and no outgoing edges is called a sink.

The In-degree of a di-graph is the number of incoming edges.

Denoted by $d^{-} (v)$ Out- degree of di-graph is the number of edges outgoing from a vertex.

Denoted by $d^{+} (v)$

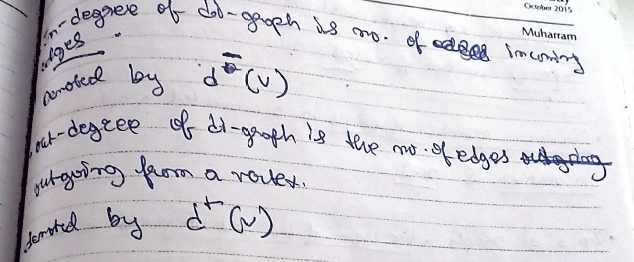
Important Terminologies

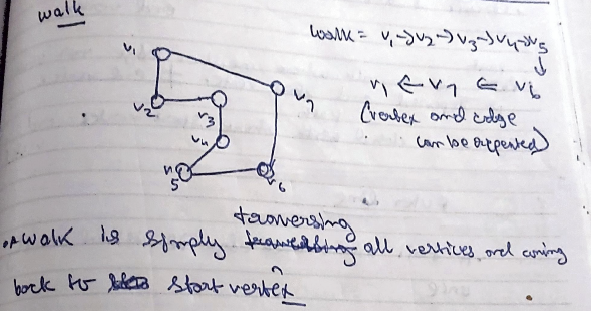
What is a Walk?

A walk is simply the traversal of all vertices in a graph and coming back to the initial vertex.

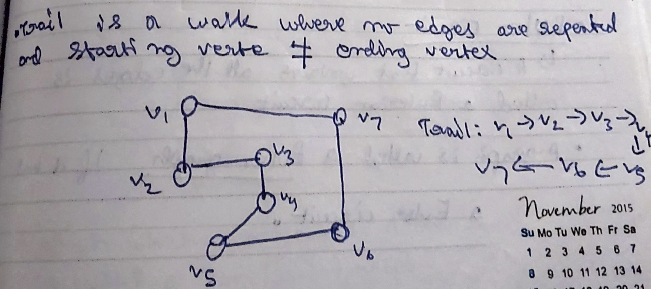
What is a Trail?

A trail is also a walk which traverses all the vertices and ending at the last vertex, where no edges are repeated and the starting vertex is not equal to the ending vertex.

What is a Circuit?

A circuit is a closed trail where the starting vertex is the same as the ending vertex, i.e the walk ends at the initial vertex (no edges are repeated).

What is a Path?

A path is a walk where neither edges nor vertices are repeated and the start vertex is not equal to the end vertex, i.e the walk ends at the last vertex of the graph.

What is a Cycle?

A cycle is a =closed Path= where the =starting vertex is the same as the ending vertex= , i.e =the walk ends at the initial vertex of the graph=.

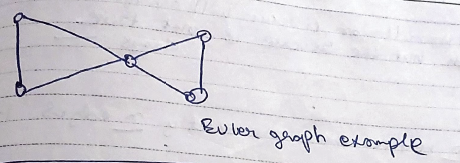
Euler Line, Eulerian Circuit and Euler Graph

What is a Euler line?

A Euler line is a trail where each edge is visited exactly once.

What is a Eulerian Circuit?

A circuit that contains all the edges(without repeating any) is called a Eulerian circuit.

What is a Euler graph?

A graph that contains a Eulerian circuit is called a Euler Graph.

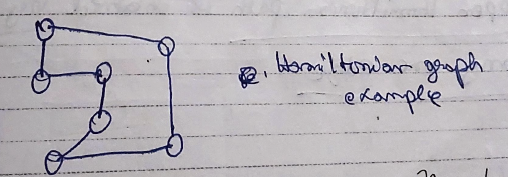
Hamiltonian path, Hamiltonian Circuit and Hamiltonian Graph

What is a Hamiltonian path?

A path which obtains every vertex of a graph exactly once is called a Hamiltonian Path.

What is a Hamiltonian circuit?

A circuit which passes through every vertex at least once is called a Hamiltonian circuit.

What is a Hamiltonian graph?

A graph which contain a Hamiltonian circuit is called a Hamiltonian graph.

Note : A Hamiltonian circuit will always have a Hamiltonian path but the reverse is not always true.

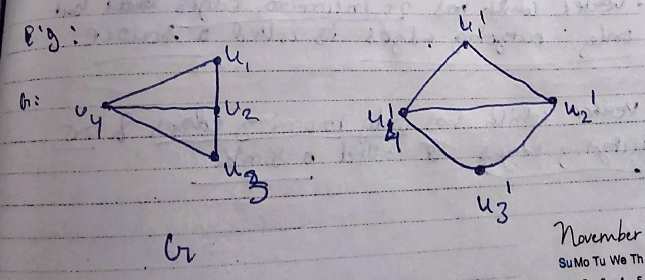
Isomorphic Graphs

Two graphs G and G’ are said to be isomorphic if

They have the same number of edges.
They have the same number of vertices.
The vertices in graph G’ should have the same degree as the vertices in the graph G.

Vertex-disjoint and Edge disjoint Graphs

Two graphs called vertex disjoint if they have no vertex in common .

Two graphs are called edge disjoint if they have no edge in common .

Theorems of Graph Theory (Semester 3)

1. Handshaking Theorem/ The first theorem of graph theory.

This theorem states that the “sum of the degree of the vertices of a graph is equal to the number of edges in a graph G”.

2. The degree of any vertex in a simple graph with any vertices is n-1.

3. ==The maximum number of edges in a connected simple graph with n vertices is :

n(n-1)/2==.

4. The number of odd vertices in any graph is even.

5. Minimum number of edges in a connected graph with n vertices in n-1.

Semester 4.

Weighted Graphs

What is a weighted graph?

A graph is called a weighted graph if a non-negative integer W(e) associates to each edge and this W(e) is a weight of corresponding edge.

In simple terms, each is edge in the graph is assigned a number.

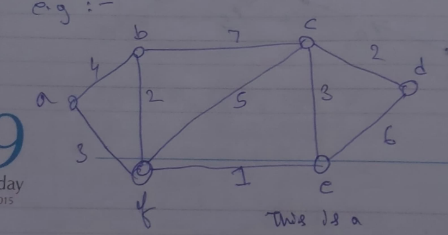
“This is a” — weighted graph.

Pathfinding algorithms and using them to find the shortest distances between vertices in weighted graphs.

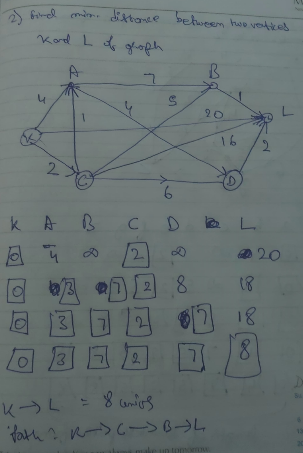
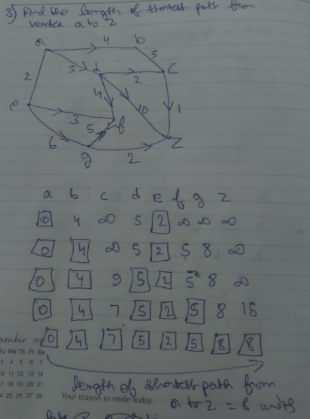
Dijkastra’s Algorithm

Dijkastra’s algorithm is a path finding algorithm which is used to find the shortest distance between two vertices. It works by calculating the short distances between intermediate vertices and finding the shortest overall distance (by summing up the intermediate distances) between the desired two vertices.

Best explained with an example :

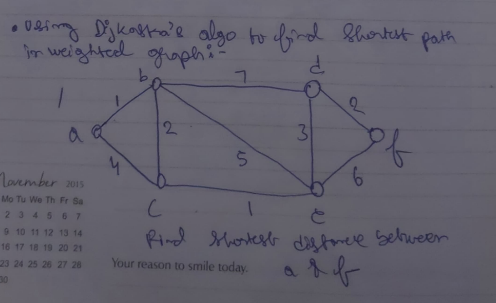
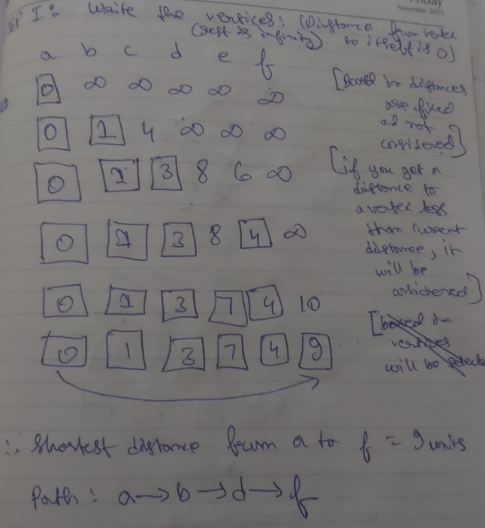
Step 1 : Write all the vertices, taking the distance of the first vertex to itself as 0 and the distances to the other vertices as infinity for the time being.

Step 2: Start working your way from the first vertexand find the shortest possible distance from the first vertex to the next vertex.

Box-in the distance of the current vertex (0). Now that it is boxed-in this distance is fixed and won’t be considered for future (except for summing up the total path length).

Keep boxing-in the shortest distances between the vertices and work your way to the last/desired vertex.

Note that if you already have found a distance from one vertex to another and then you find another, which happens to be greater than the current, the newly found distance won’t be considered. Instead the shorter one will be boxed-in

Step 3: Once you have found the shortest distance from the first vertex to the desired one, you can simply write it down.

For further clarification : Video link(Recommended to watch) : https://www.youtube.com/watch?v=iOu3PXv5L6w&list=PLU6SqdYcYsfLV24T0XVb3z3mjl8QG0EBN&index=6

More examples

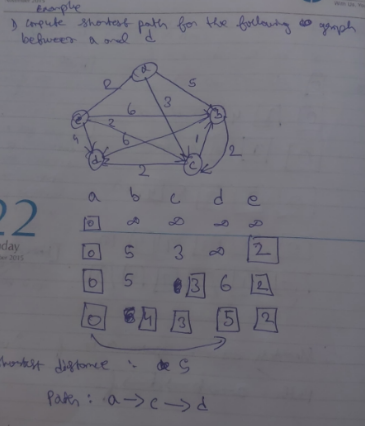
Graph Coloring

Coloring of Vertices

Coloring of graph G means coloring of vertices with different colors.

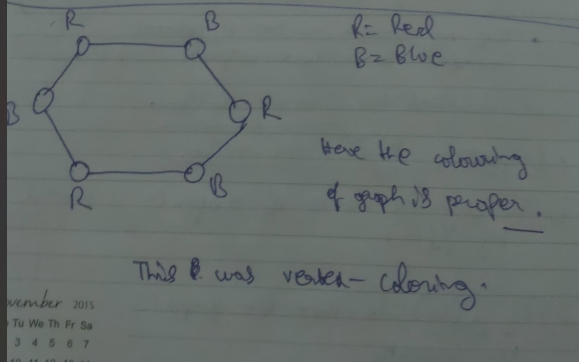
Proper vertex coloring of graphs

The coloring of a graph is Proper if any two adjacent vertices u and v have two different colors.

The minimum number of colors needed to produce a proper coloring is called the chromatic number or vertex chromatic number or the vertex chromatic index.

Denoted by :

$χ (G)$

Properties of vertex Chromatic number

Coloring of Edges

Same as vertex coloring, edge coloring is the assignment of colors to the edges of a graph G so that adjacent edges are colored differently.

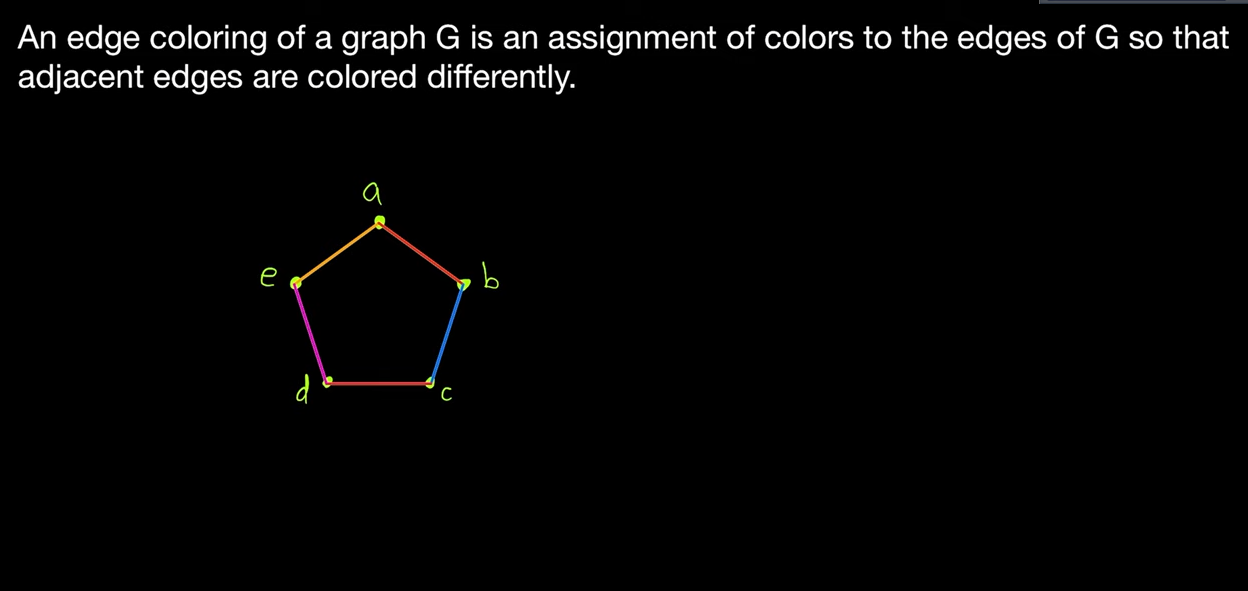Same as proper vertex coloring, proper edge coloring happens when no two adjacent edges have the same color.

Same as the vertex chromatic number, the minimum number of colors needed to produce a proper edge coloring is called the edge chromatic number or the edge chromatic index.

Denoted by

$χ^{'} (C_{5})$ where $C_{5}$ denotes the coloring of the 5 edges.

If k colors are sufficient to color a graph G then graph is said to be k-colorable .

$k = χ^{'} (G)$

Then G is said to be k-edge-chromatic.

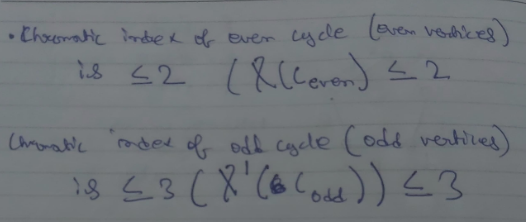
Coloring Maps

Coloring maps is a specific application of graph coloring, which involves assigning colors to regions on a map such that no two adjacent regions share the same color. This problem is often modeled using a graph where each region is represented as a vertex and an edge connects two vertices if their corresponding regions share a boundary.

Theorems of Coloring Maps:

The Four color theorem: A famous result in map coloring is the Four Color Theorem, which states that any planar map can be coloued with at most four colors such that no two adjacent regions have the same color.

Let there be a map with the following region:

where no adjacent regions can have the same color.

So according to the four color theorem :

To color the different regions of any map, there is no requirement of more than 4 different colors.

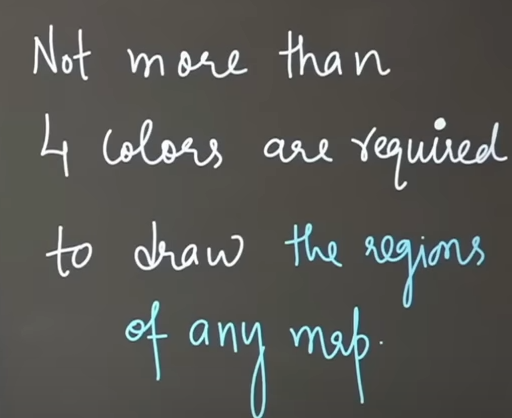
The Five color theorem : The Five Color Theorem is a result in graph theory related to coloring maps and planar graphs. It states that any planar graph (or equivalently, any map where each region is a contiguous area) can be colored using no more than five colors in such a way that no two adjacent regions (regions sharing a boundary segment, not just a point) share the same color.

Perfect Graph

Trees

A tree is a connected graph without any loops or circuits.

Example :

Rooted Tree

A rooted tree is a tree in which vertex acts as the root(initial vertex) of the tree.

Binary Tree

A binary tree is defined as a tree in which there is exactly one vertex of degree two which acts as the root vertex and the remaining vertices could be of degrees one or three but not two.

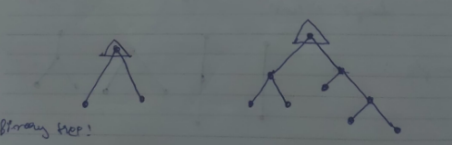
These are binary trees.

However

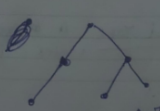
This is not a binary tree as there is one vertex other than the root which has a degree of 2.

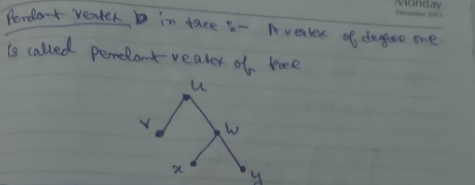
The vertices at the end of the tree are called pendant vertices since they have a degree of 1.

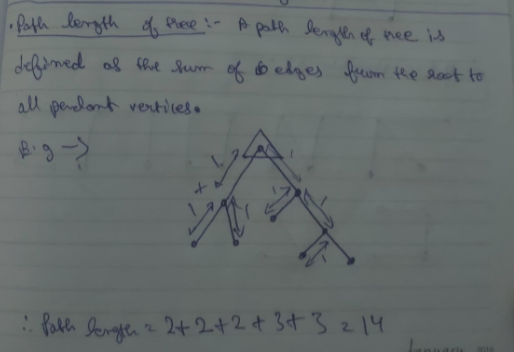
Path length of a tree

A path length of a tree is defined as the sum of edges from the root to all the pendant vertices.

Spanning Trees

Video explanation (Recommended to watch) :

https://www.youtube.com/watch?v=f30rxGvPWPo&list=PLU6SqdYcYsfLV24T0XVb3z3mjl8QG0EBN&index=9

A spanning tree is basically a subgraph of a graph G.

ST = Spanning Trees

Some examples on Spanning Trees

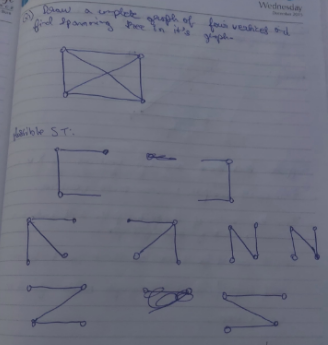
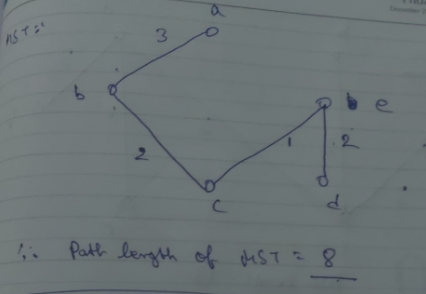
Minimal Spanning Trees

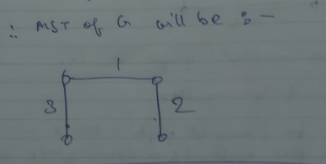
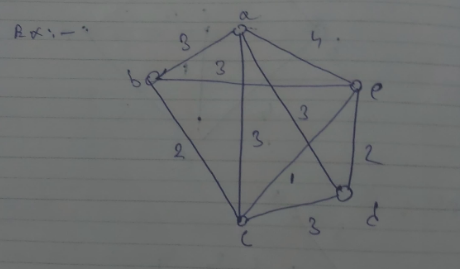
Let G be a weighted graph. A minimal spanning tree of G is a spanning tree of minimum weight.

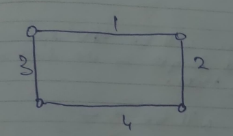
Graph G.

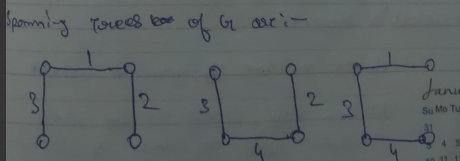
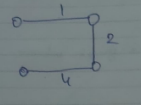
However the MST of G will be the spanning tree whose combined length is the least of all the spanning trees.

Algorithms for finding the MST of a Tree.

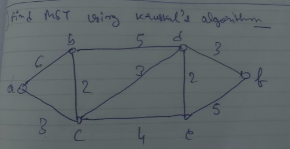
1. Kruskal’s Algorithm

Step 1. Choose an edge of minimal weight. Step 2. At each step, choose the edge whose inclusion will not create a circuit. Step 3. If a graph G has n vertices then stop after (n-1) edges.

Example of Kruskal’s algorithm:

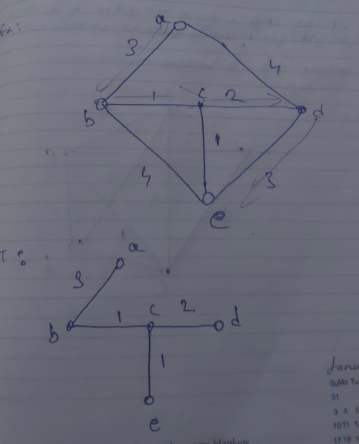
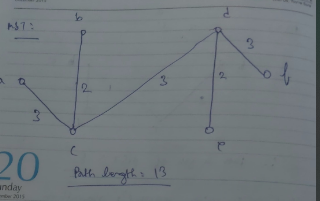
2. Prim’s Algorithm

Step 1. Select any vertex and choose the edge and smallest weight from G.

Step 2. At each stage choose the edge of smallest weight, don’t connect the vertices which are already connect with the smallest weight.

Step 3. Continue till all vertices are included.

Example of Prim’s Algorithm :

Articulation Points and Bi-connected components.

Video explanation (Recommended to watch) : https://www.youtube.com/watch?v=jFZsDDB0-vo

In a graph, if there any vertex, whose removal will disconnect the graph into multiple components then that vertex is known as an Articulation Point

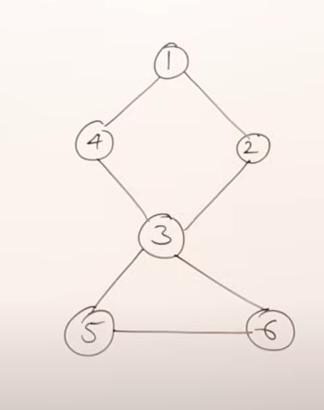
For example in this graph, the vertex 3 is an Articulation point since it’s removal will cause the graph to split into two components.

So Articulation points are un-desirable in graphs.

Articulation points can be resolved by the introduction of Bi-connected component(s).

The Bi-connected component is achieved by simply joining two available vertices other than the currently existing Articulation point so that even if that point breaks, the two halves of the graph will still be connected.

In this instance, the Bi-connected component is achieved by :

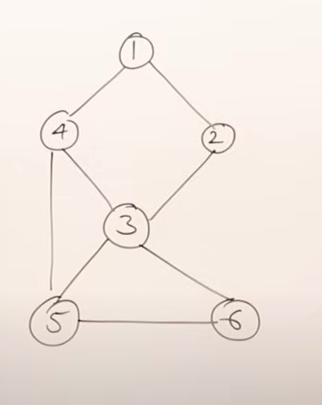
simply joining vertices 4 and 5 .

🪴 Quartz 4.0

Explorer

Graph Theory -- Semester-4