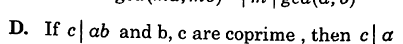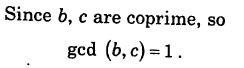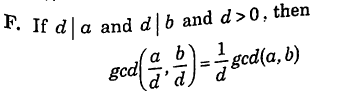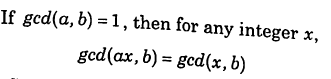Before you start reading :
This is fairly easy to understand. Just don't be afraid of symbols and have patience while reading, read slowly, but not too slow.
If it seems too hard just memorize the proofs.
Mathematical Induction
Mathematical induction is a proof technique used in mathematics to establish the truth of an infinite number of statements. It is particularly useful for proving propositions that are asserted for all natural numbers. The method works by proving two main steps:
- Base Case: Show that the statement holds for the initial value of the sequence (usually n=0 or n = 1).
- Inductive Step: Show that if the statement holds for some arbitrary natural number k, hen it also holds for k+1
Principle of mathematical induction
For a statement P(n), involving the natural number n, such that:
P(1) is true
Truth of P(k) implies the truth of P(k+1), then P(n) is true for all natural numbers n.
Example (Don’t overstress it)

Well-Ordering Principle
Using the principle of mathematical induction the well ordering principle states that :
“Every non-empty subset of natural numbers (N) has a smallest element.”
Proof :
If S be a non-empty subset of natural numbers then there exists a :
A set containing just one element has a smallest number, namely the element itself. Hence the well-ordering principle is true for a set of size 1.
Now let us assume that the principle is true for a set of size n, i.e any set of n natural numbers has a smallest number.
Let us now consider a set S of (n+1) elements where an element p is removed. The remaining n (since an element was removed, n+1 - 1 = n) numbers has a smallest element say q [by the induction hypothesis] (where we assume the statement to be true for some arbitrary integer k, being q in this case)
The smaller of p and q is the smallest element of S.
Hence, by the principle of mathematical induction, the well-ordering principle follows that any non-empty infinite set of natural numbers, has a smallest element.
Divisibility Theorem
An integer b is divisible by an integer a (not equals to zero), if there is an integer x such that :
, we write :
i.e (a is divisible by b).
In case a is not divisible by b, we write :
When a divides b, a is called a divisor/ factor of b
and b is called a multiple of a.
If
then since
Thus
Some properties of divisibility (don’t overstress it)

Prime Numbers — What are they?
A positive integer p>1 is called prime if the only positive factors of p are p itself and 1.
If a positive integer n>1 is not prime then it is called a composite number.
1 is neither prime nor composite.
The only even prime integer is 2, rest all prime integers are odd.
If n is a composite integer then there exists integers a and b such that
where 1<a, b, n
Fundamental theorem of arithmetic
The fundamental theorem of arithmetic states that:
“Every integer n can be expressed uniquely as a product of primes”.
Proof :
If the integer n > 1 is a prime then the integer itself stands a product of a single factor.
Otherwise, if the integer n is not prime, it can be factored into, let’s say :
where
and
Well obviously the factors are gonna be less than n itself and greater than 1.
Now,
If n1 is a prime : then let it stand (JoJo reference) else:
n1 will be factored similarly into, let’s say :
where
and
and the process goes on…
This process of writing each composite number as a product of factors must terminate since the factors are smaller than the composite number itself and greater than 1.
Thus every integer n, such that n > 1 can be written as a product of primes.
This process is called prime decomposition or the prime factorization of n.
Now,
if there be :
prime factors of n, each equal to
then, n can be written as
Or in simple terms, see the below example :
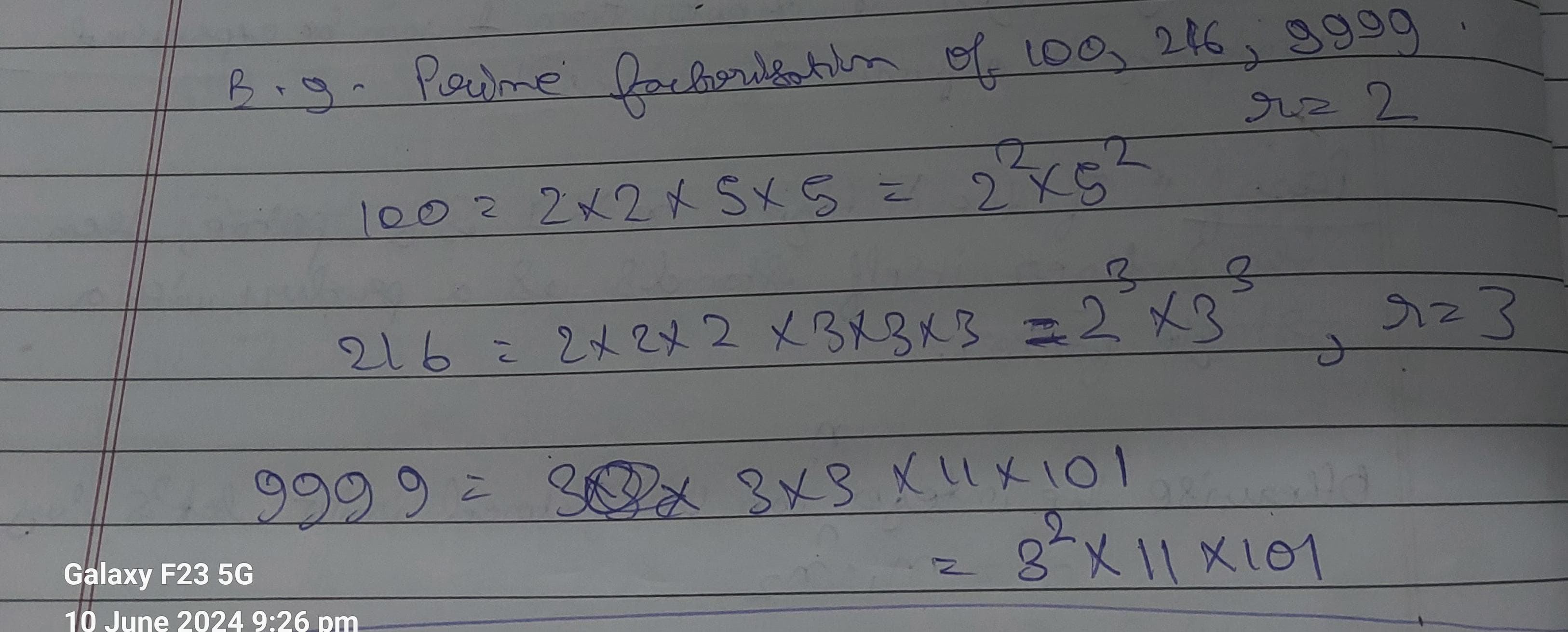
In the first example, n = 100 which is broken down into n1, n2, n3, n4, further assembled in the form of:
where
r = 2.
Prime Numbers : Euclid’s theorem.
Euclid’s theorem states that :
“The number of prime numbers are infinite”
Proof:
If possible, let the number of primes be finite and be equal to n. Let them be arranged in the order of magnitude as :
Then form the number :
Now, no single p is a divisor of n.
Therefore, n is : either a prime greater than or has a prime greater than as a factor.
But this contradicts our assumption that is the greatest prime (fraud).
Therefore, the number of prime numbers is infinite. Proved
The division algorithm
The division algorithm of prime numbers states that :
Given any two integers a and b, with b > 0, there exists unique integers q and r such that
where,
Proof : TLDR (Too long don’t read), still providing :
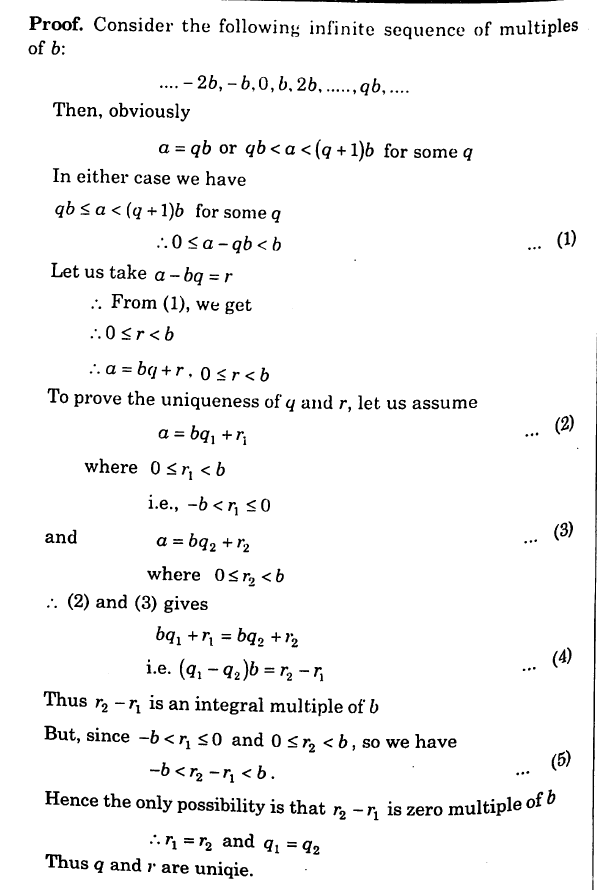
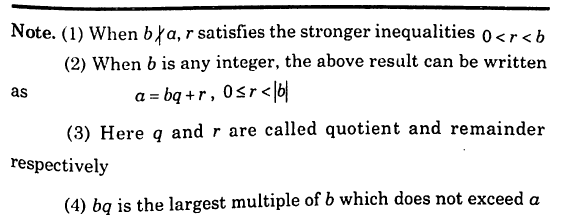
Key Takeaway of the division algorithm :
Read what it implies (not the proof)
Read the Note part just above and
Just see the examples :
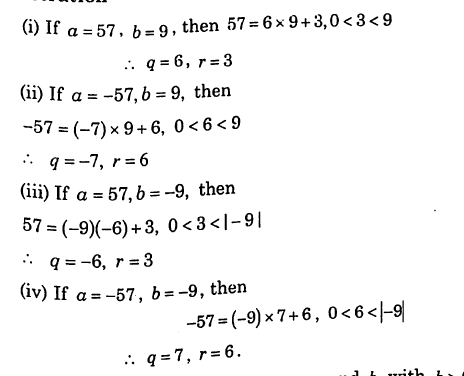
The Greatest Common Divisor (GCD)
Definition (Pay attention to this one)
The integer d,:
is said to be the common divisor of integers a and b if
and , that is if d divides both a and b
Euclidean algorithm of finding GCD
Proof : TLDR


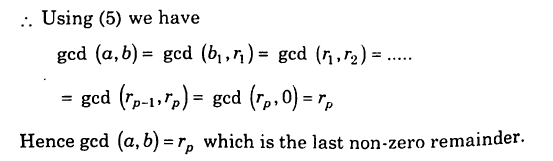
Examples (Key takeaway)

Properties of GCD
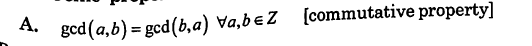
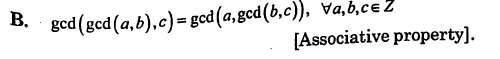
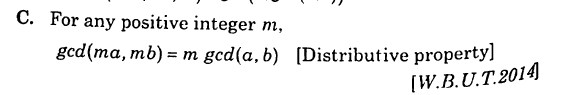
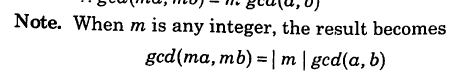
Any integer being m could be negative as well