Index
- Introduction to Code Optimization
- Loop Optimization
- Control Flow Graphs, Basic Blocks and identifying loops within Basic Blocks
- Transformation of basic blocks and DAG representation of basic blocks
- Directed Acyclic Graph (DAG) representation of basic blocks
- Peephole Optimization
Introduction to Code Optimization
https://www.youtube.com/watch?v=O5YlRUYFDA8&list=PLxCzCOWd7aiEKtKSIHYusizkESC42diyc&index=25
Code optimization is a crucial phase in the compilation process, aiming to improve the performance and efficiency of the intermediate code without changing its functionality. It makes the program:
- Faster: By reducing the number of instructions or improving execution patterns.
- Smaller: By eliminating redundant instructions to save memory.
- Efficient in Resource Utilization: By minimizing CPU registers, memory access, and I/O operations.
Goals of Code Optimization
- Improve Execution Time: Reduce the runtime of the compiled program.
- Minimize Resource Utilization: Use CPU registers and memory efficiently.
- Reduce Power Consumption: Particularly important in mobile and embedded systems.
- Preserve Correctness: Ensure the program’s output remains consistent with the unoptimized version.
Types of Code Optimization

In our syllabus we have Peephole Optimization and Loop Optimization.
Common Optimizations
- Dead Code Elimination: Remove instructions or code that do not affect the program’s output.
- Example :
int x = 5;
x = 10; // 'x = 5' is dead code.- Constant Folding: Precompute constant expressions at compile time.
- Example:
int x = 5 * 4; // Replace with 'int x = 20'.-
Strength Reduction: Replace expensive operations with equivalent, cheaper ones.
- Example: Replace multiplication (
x * 2) with addition (x + x).
- Example: Replace multiplication (
-
Loop Optimization: Improve loop efficiency by techniques like loop unrolling, loop fusion, or invariant code motion.
-
Inline Expansion: Replace a function call with its body to avoid the overhead of the call.
Importance of Code Optimization
- Improved User Experience: Faster programs lead to better performance.
- Reduced Cost: Saves resources like memory and power.
- Necessary for Embedded Systems: Optimized code is essential for systems with limited resources.
- Competitive Advantage: Efficient software is often a selling point in the industry.
Loop Optimization
Loop Optimization is the process of increasing execution speed and reducing the overheads associated with loops. It plays an important role in improving cache performance and making effective use of parallel processing capabilities. Most execution time of a scientific program is spent on loops.
https://www.youtube.com/watch?v=AKYuP3vpdlg&list=PLxCzCOWd7aiEKtKSIHYusizkESC42diyc&index=27
Loop Optimization Techniques
Now, there are various loop optimization techniques, most well-known are these three methods :
1. Code Motion (Frequency Reduction)
In frequency reduction, the amount of code in the loop is decreased. A statement or expression, which can be moved outside the loop body without affecting the semantics of the program, is moved outside the loop.

Here we see that within the loop :
a = 100;
while(a>0) {
x = y + z;
if(a % x == 0) {
printf("%d", a);
}
}We see that the like x = y + z is being repeatedly called within it’s loop while it’s value (value of x) doesn’t change anywhere after that line, and is just being read in the line (if(a % x == 0)).
So we could modify the code to look like this instead :
a = 100;
x = y + z;
while(a>0) {
if(a % x == 0) {
printf("%d", a);
}
}So the essential output of the code remains the same, while the needless looped addition calculation of x is factored out in the new code.
Or here’s another example :
Before optimization:
while(i < 100) {
a = Sin(x) / Cos(x) + i;
i++;
}After optimization:
t = Sin(x) / Cos(x);
while(i < 100) {
a = t + i;
i++;
}2. Loop Fusion/Loop Jamming
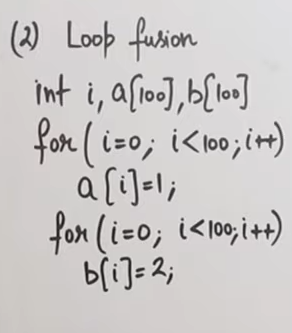
So currently we see two loops with the exact same condition. And each loop has an executing statement.
This state of the code which it is currently in, is called Loop Fission.
Loop Fission :
Loop fission improves the locality of reference, in loop fission a single loop is divided into multiple loops over the same index range, and each divided loop contains a particular part of the original loop.
Before optimization:
for(x=0; x<10; x++){
a[x] = 1
b[x] = 5
}After optimization:
for(x=0; x<10; x++){
a[x] = 1
}
for(x=0; x<10; x++){
b[x] = 5
}Now the reverse of this is called Loop Fusion or Loop Jamming.
In the given code :
int i, a[100], b[100]
for(i = 0; i < 100; i++) {
a[i] = 1;
}
for(i = 0; i<100; i++) {
b[i] = 2;
}We see that two segments of code a[i] = 1 and b[i] = 2, are spread out over two for-loops with the same looping conditions.
So we can optimize this loop by merging the two segments in a single for loop.
int i, a[100], b[100]
for(i = 0; i < 100; i++) {
a[i] = 1;
b[i] = 2;
}The fusion and fission of loops depends on the use-case of the program and the given scenario in general.
3. Loop unrolling
Loop unrolling is a loop transformation technique that helps to optimize the execution time of a program. We basically remove or reduce iterations. Loop unrolling increases the program’s speed by eliminating loop control instruction and loop test instructions.

Here we see, in this piece of code that the loop stretches out for a very short amount of time.
So instead of looping, which will cost more resources, we can simply write:
printf("Varun");
printf("Varun");
printf("Varun");
printf("Varun");
printf("Varun");which doesn’t alter the semantics of the program at all.
Control Flow Graphs, Basic Blocks and identifying loops within Basic Blocks
https://www.youtube.com/watch?v=tKnNqiU4gCI&list=PLxCzCOWd7aiEKtKSIHYusizkESC42diyc&index=28
So, control flow graphs are used to detect loops in the low-level code, that is when the intermediate code is converted to a TAC (Three-Address-Code) form.
Flow Graph
A flow graph is a directed graph where:
- Each node represents a basic block.
- Each edge represents the control flow between basic blocks (i.e., jumps and branches).
Components of a Flow Graph:
- Nodes: Represent basic blocks.
- Edges: Represent possible transitions between blocks.
- Entry Block: The starting block of the program.
- Exit Block: The block where the program ends.
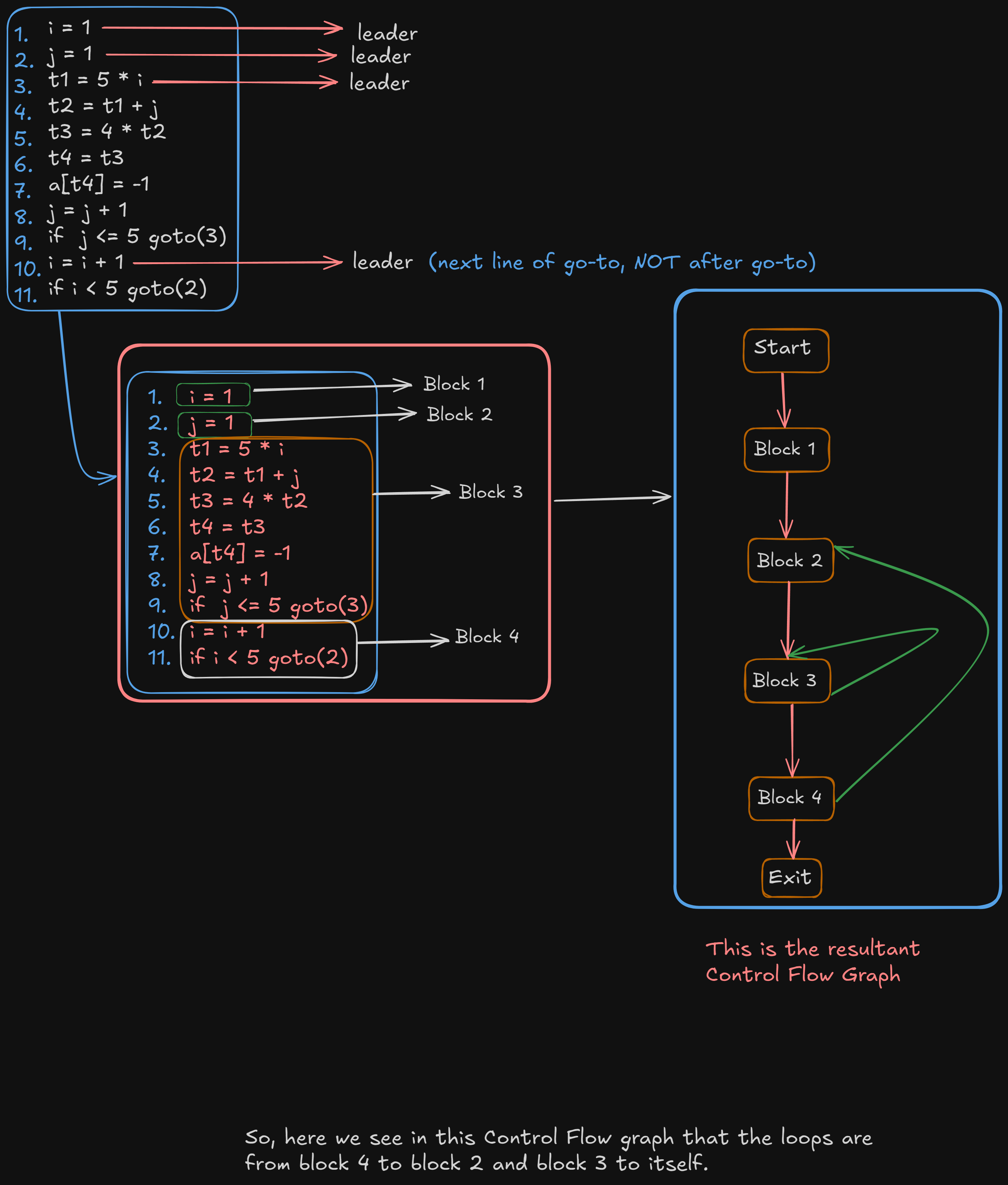
Let’s understand the part of Control Flow Graphs and Basic Blocks with an example.

So we have this intermediate code in the form of TAC.
We need to construct a Control-Flow Graph and identify loops within the code.
To do that, we need to follow some rules :

So first things first, what is a leader?
Leaders are the leading statements in a block, which are often indicators for the beginning of loop blocks as well.
Each block can have only one leader.
Basic Block Construction
To create basic blocks, follow these steps:
-
Identify leaders (the first instruction of a basic block):
- The first instruction of the program.
- Any instruction that is the target of a jump or branch.
- Any instruction following a jump or branch.
-
Group consecutive instructions between leaders into blocks.
Here’s a really nice video example explaining that process in detail :
https://www.youtube.com/watch?v=tkSsh91ehUA&list=PLxCzCOWd7aiEKtKSIHYusizkESC42diyc&index=29
So in this code:
i = 1
j = 1
t1 = 5 * i
t2 = t1 + j
t3 = 4 * t2
t4 = t3
a[t4] = -1
j = j + 1
if j <= 5 goto(3)
i = i + 1
if i < 5 goto(2)The resultant Control Flow Graph will be :
Advantages of Using Basic Blocks and Flow Graphs
- Simplified Analysis: Allows the compiler to reason about the program’s structure.
- Foundation for Optimization: Enables techniques like dead code elimination, common subexpression elimination, etc.
- Clear Representation: Makes control flow more understandable for transformations.
Applications in Optimization
- Dead Code Elimination: Identify unreachable blocks and remove them.
- Loop Detection: Easily identify loops by finding cycles in the flow graph.
- Control Flow Analysis: Determine how the program moves from one block to another.
- Data Flow Analysis: Analyze how variables and data are used across blocks.
Transformation of basic blocks and DAG representation of basic blocks
https://www.geeksforgeeks.org/optimization-of-basic-blocks/
This is also known as optimization of basic blocks. Optimization is the process of transforming a program that improves the code by consuming fewer resources and delivering high speed. In optimization, high-level codes are replaced by their equivalent efficient low-level codes.
There are two types of basic block optimizations:
- Structure preserving transformations
- Algebraic transformations
Structure-Preserving Transformations:
The structure-preserving transformation on basic blocks includes:
- Dead Code Elimination
- Common Subexpression Elimination
- Renaming of Temporary variables
- Interchange of two independent adjacent statements
1. Dead Code Elimination:
Dead code is defined as that part of the code that never executes during the program execution. So, for optimization, such code or dead code is eliminated. The code which is never executed during the program (Dead code) takes time so, for optimization and speed, it is eliminated from the code. Eliminating the dead code increases the speed of the program as the compiler does not have to translate the dead code.
Let’s understand this with an example :
// Program with Dead code
int main()
{
x = 2
if (x > 2)
cout << "code"; // Dead code
else
cout << "Optimization";
return 0;
}Here we see that the block :
if (x > 2)
cout << "code"; is dead code since the value of x is fixed at 2.
So we can simply remove that part of code,
// Optimized Program without dead code
int main()
{
x = 2;
cout << "Optimization"; // Dead Code Eliminated
return 0;
}To get an optimized version of the code.
2. Common Subexpression Elimination:
In this technique, the sub-expression which are common are used frequently are calculated only once and reused when needed. DAG ( Directed Acyclic Graph ) is used to eliminate common subexpressions.
For example :
In this regular expression : x = (a + b) + (a + b) + c
If we were to convert this to a TAC then generate a control flow graph :
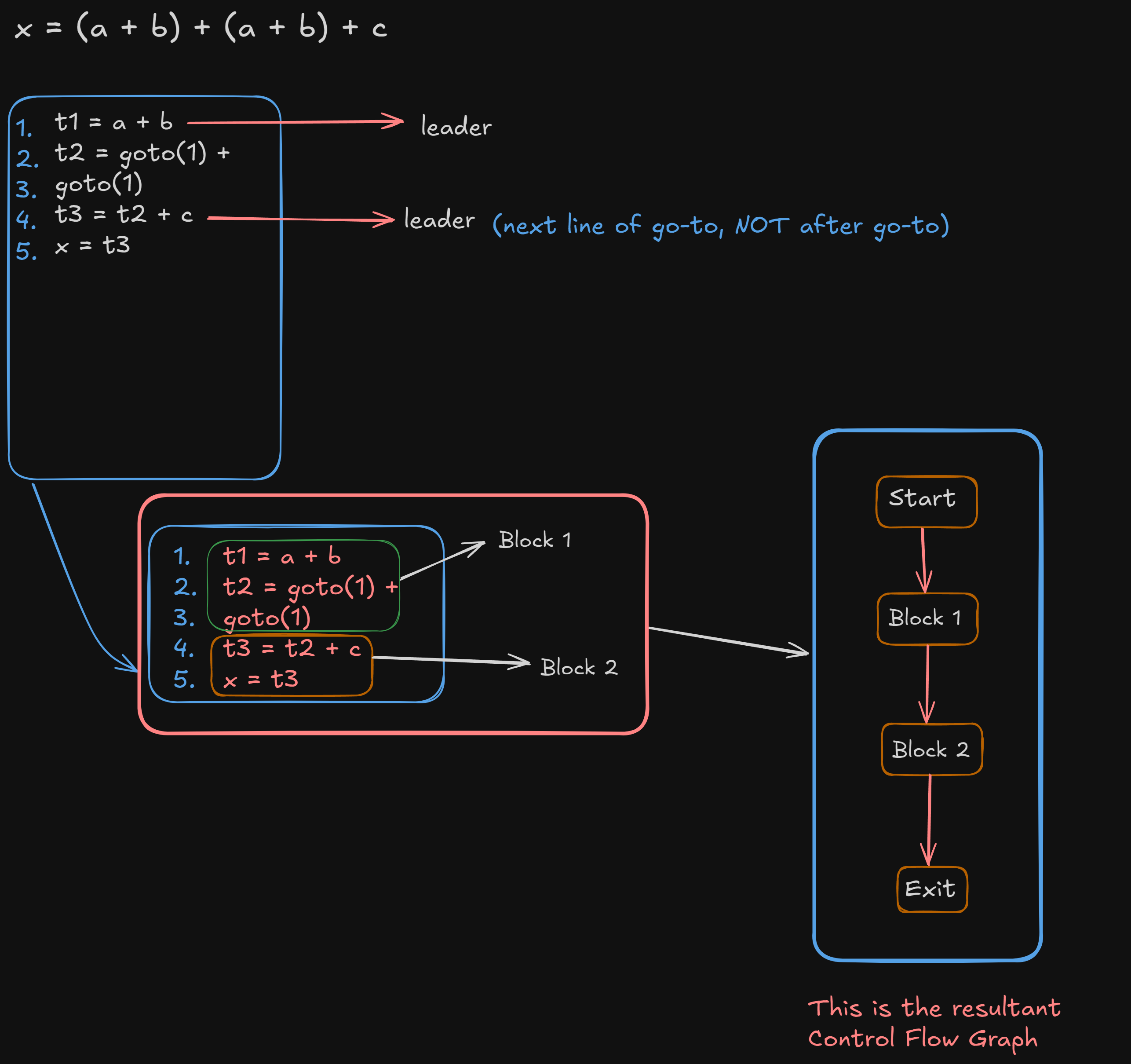
We can see that a+b is being referenced twice, which means it’s a common sub-expression.
Representing it in an AST would be :
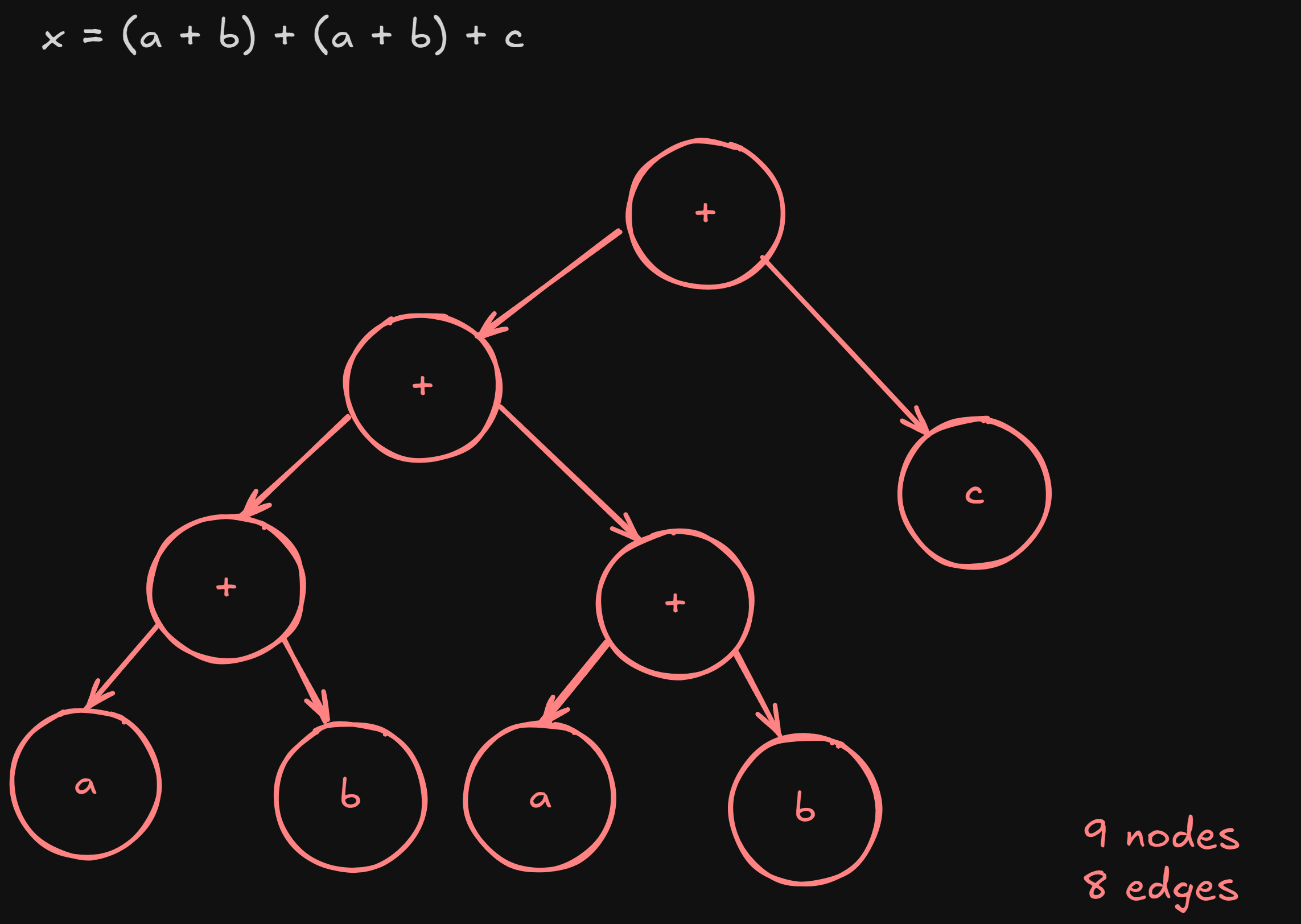
Now, if we represent this using a Directed Acyclic Graph and eliminate the common subexpression a+b,
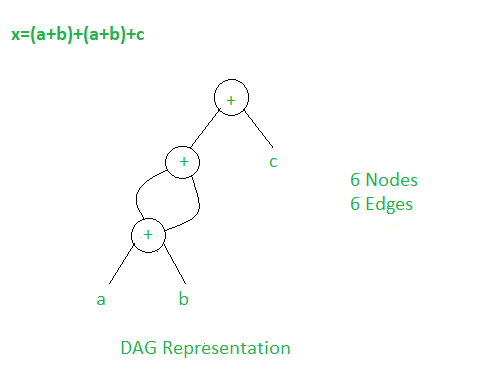
The basic block is now a lot more optimized.
3. Renaming of Temporary Variables:
Statements containing instances of a temporary variable can be changed to instances of a new temporary variable without changing the basic block value.
Example: Statement t = a + b can be changed to x = a + b where t is a temporary variable and x is a new temporary variable without changing the value of the basic block.
4.Interchange of Two Independent Adjacent Statements:
If a block has two adjacent statements which are independent can be interchanged without affecting the basic block value.
Example:
t1 = a + b
t2 = c + dThese two independent statements of a block can be interchanged without affecting the value of the block.
Algebraic Transformation:
Countless algebraic transformations can be used to change the set of expressions computed by a basic block into an algebraically equivalent set. Some of the algebraic transformation on basic blocks includes:
- Constant Folding
- Copy Propagation
- Strength Reduction
1. Constant Folding:
Solve the constant terms which are continuous so that compiler does not need to solve this expression.
Example:
x = 2 * 3 + y ⇒ x = 6 + y // (Optimized code)2. Copy Propagation:
It is of two types, Variable Propagation, and Constant Propagation.
Variable Propagation:
x = y
z = x + 2can be optimized as
z = y + 2 // using variable y instead and discarding xConstant Propagation:
x = 3
z = x + acan be optimized as:
z = 3 + a // 3 is a constant3. Strength Reduction:
Replace expensive statement/ instruction with cheaper ones.
x = 2 * y (costly) ⇒ x = y + y (cheaper)
x = 2 * y (costly) ⇒ x = y << 1 (cheaper)3. Loop Optimization.
Stuff which was done in Loop Optimization
Directed Acyclic Graph (DAG) representation of basic blocks
Just watch this video : https://www.youtube.com/watch?v=eWleNdT92VM
Peephole Optimization
https://www.youtube.com/watch?v=clb4tnEm8l4&list=PLxCzCOWd7aiEKtKSIHYusizkESC42diyc&index=24
Peephole Optimization is a local optimization technique performed at the level of small sets of instructions (or “peepholes”) in a program. It examines short sequences of target code and tries to optimize them by replacing them with shorter, faster, or more efficient equivalents.
It basically works on the theory of replacement in which a part of code is replaced by shorter and faster code without a change in output. The peephole is machine-dependent optimization.
Objectives of Peephole Optimization:
The objective of peephole optimization is as follows:
- To improve performance
- To reduce memory footprint
- To reduce code size
Peephole Optimization Techniques:
1. Redundant load and store elimination:
In this technique, redundancy is eliminated.
Initial code:
y = x + 5;
i = y; // unncessary redundancy added here.
z = i; // unncessary redundancy added here.
w = z * 3; Optimized code:
y = x + 5;
w = y * 3; //* there is no i now
// We've removed two redundant variables i & z whose value were just being copied from one another.2. Constant Folding.
The code that can be simplified by the user itself, is simplified. Here simplification to be done at runtime are replaced with simplified code to avoid additional computation.
Initial code:
x = 2 * 3; Optimized code:
x = 6;3. Strength Reduction
The operators that consume higher execution time are replaced by the operators consuming less execution time.
Example 1
Initial code:
y = x * 2;Optimized code:
y = x + x; or y = x << 1;Example 2
Initial code:
y = x / 2;Optimized code:
y = x >> 1;4. Replace slower instructions with faster instructions

View https://www.youtube.com/watch?v=clb4tnEm8l4&list=PLxCzCOWd7aiEKtKSIHYusizkESC42diyc&index=24 to understand this better.
5. Dead Code Elimination
Dead code refers to portions of the program that are never executed or do not affect the program’s observable behavior. Eliminating dead code helps improve the efficiency and performance of the compiled program by reducing unnecessary computations and memory usage.
Initial code:
int Dead(void) {
int a=10;
int z=50;
int c;
c=z*5;
printf(c);
a=20;
a=a*10; //No need of These Two Lines
return 0;
}Optimized code:
int Dead(void) {
int a=10;
int z=50;
int c;
c=z*5;
printf(c);
return 0;
}