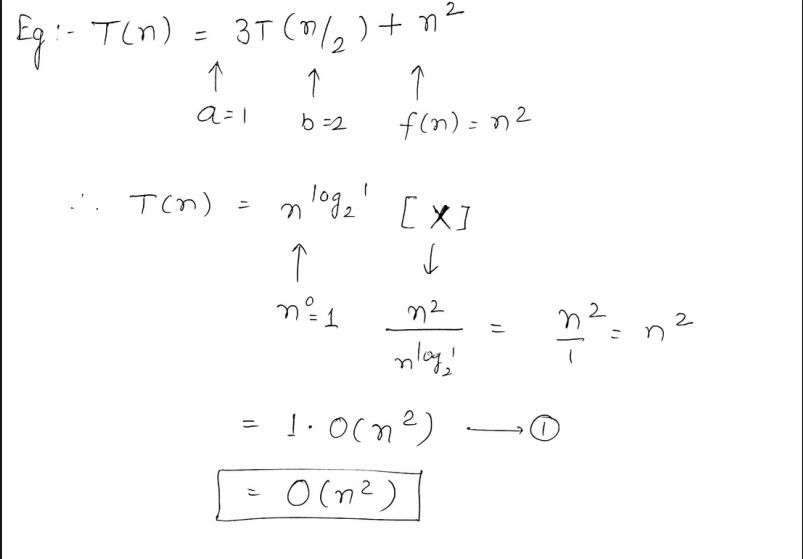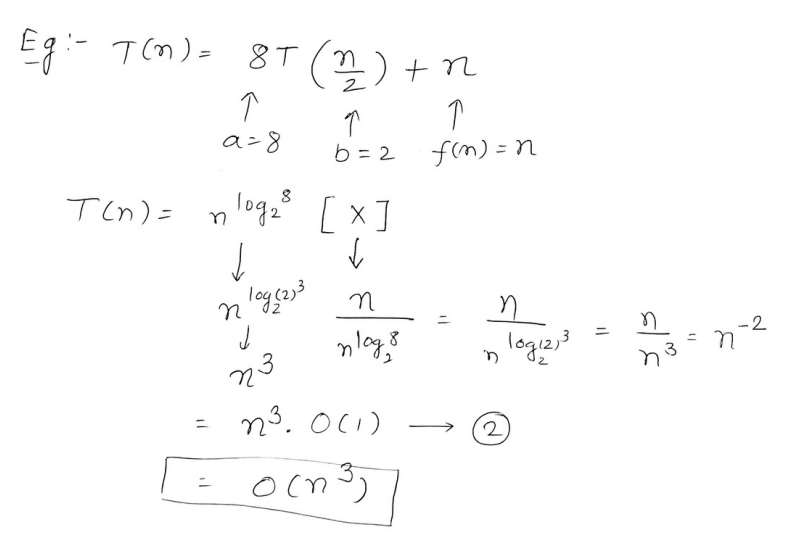What is an algorithm?

Algorithm vs Program

Complexity Bounds and Asymptotic Notations

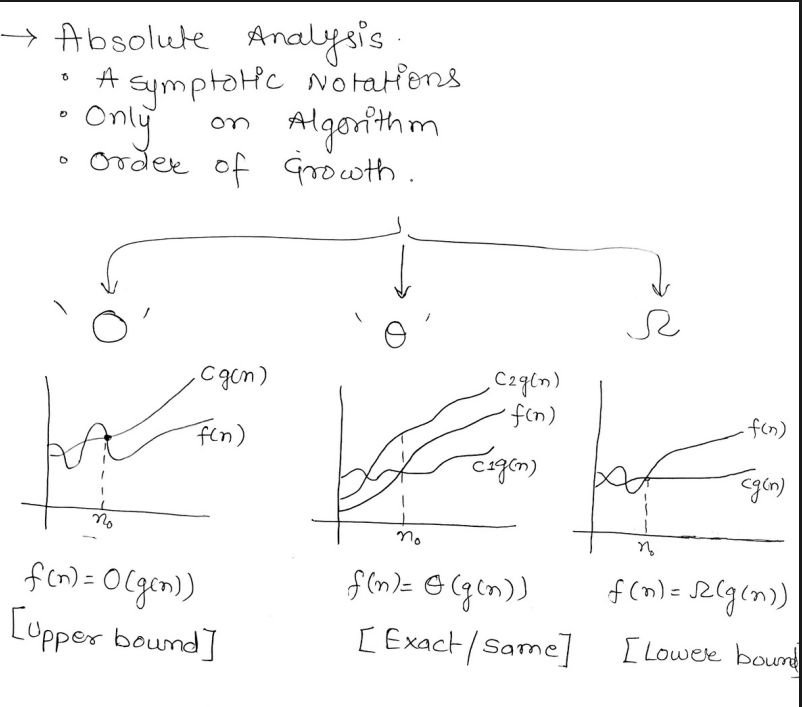
So there are 3 asymptotic notations,
- Big - O (pronounced as Big oh)
- Big - (pronounced as Big theta)
- Big - (pronounced as Big omega)
These are used in comparison of ranges, which happen to be either have an
- Upper bound
- Exact/same bound
- Lower bound
For example in the first graph we have the function is the upper bound for which means when values of ==n>== , will never be greater than , denoted by O.
Therefore = O()
In the second graph, for values of ==n>== , , which is denoted by .
Thus, =
In the third graph, for values of ==n>== , will always be lesser than , which is denoted by .
Thus .
These were the Big Notations.
There also exist small notations.
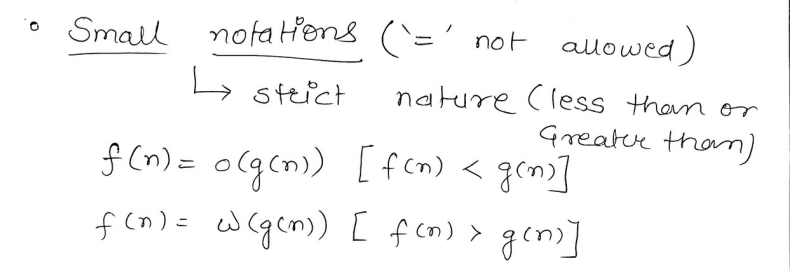
Here only small-o (small oh) and small omega exist, since only lower or greater bounds are defined by small notations, exact notations cannot be defined using small notations.
is small omega, .
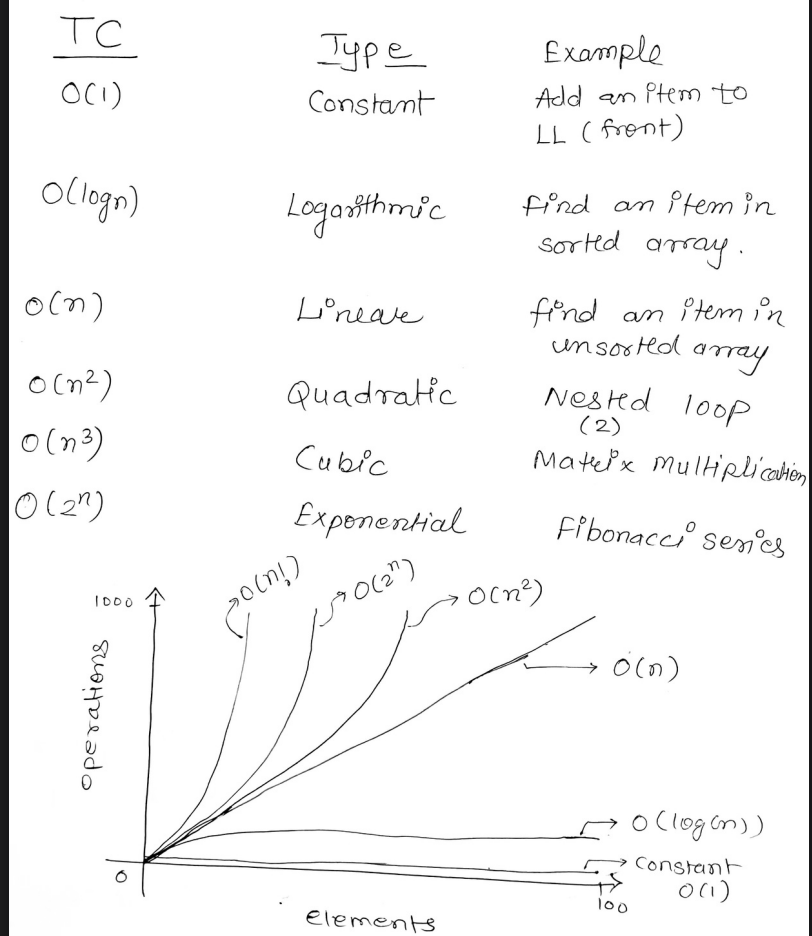
Types of Time Complexity.
Recurrence Relations

For example : The time complexity of the binary search algorithm.
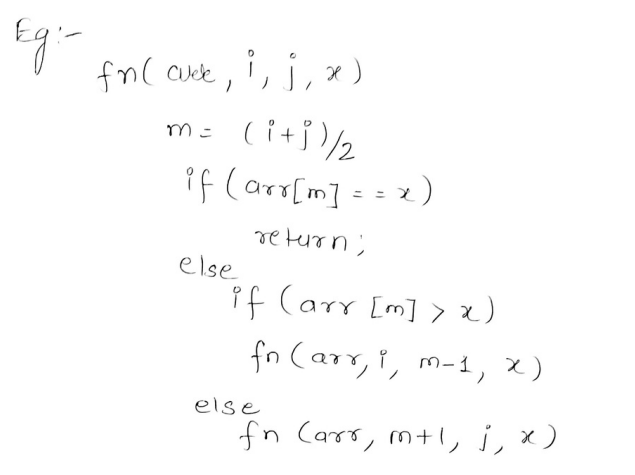
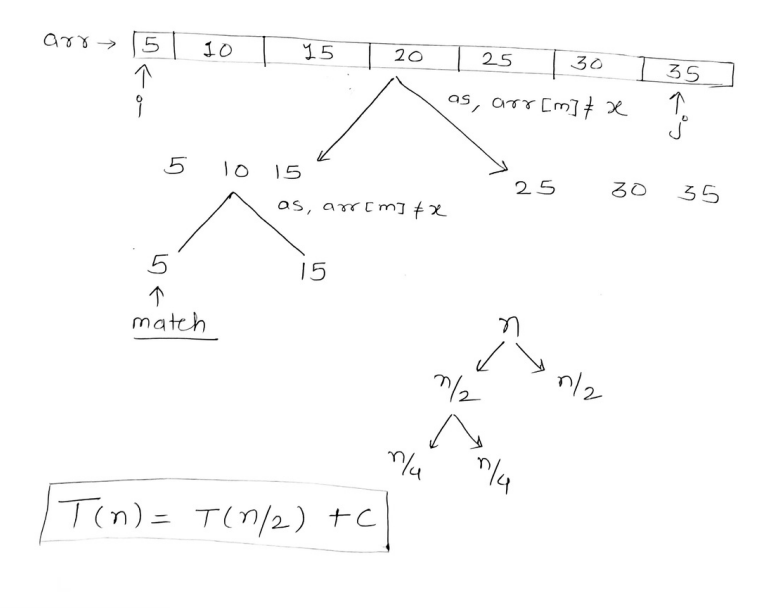
The expression is a recurrence relation and it is the recurrence relation of the binary search algorithm.
There are two major methods to solve a recurrence relation.
- Substitution Method
- Master Theorem
1. The Substitution Method
So we have the recurrence relation
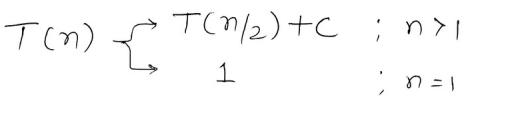
So we start by substituting
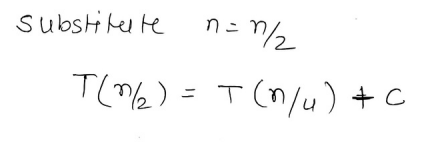
Thus ....... (i)
And then we repeat the process again for .
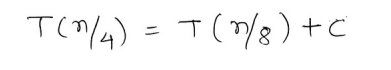
....... (ii)
Then we substitute the value of equation (i) in the original recurrence relation :
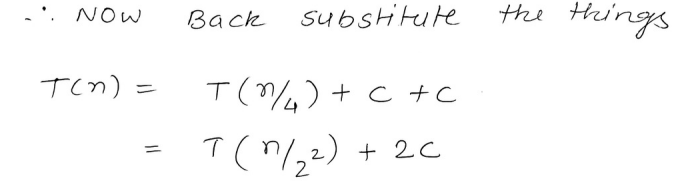
And we do the same for equation (ii) as well.
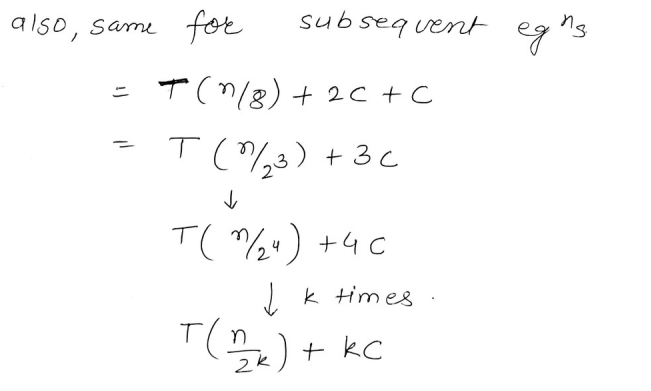
And thus we see that a pattern approaches with this equation :
.....(iii)
Let’s set equation equal to 1.
Therefore, = 1
or = n.
Therefore we get :
or
This gets reduced to
which is further reduced to
O()
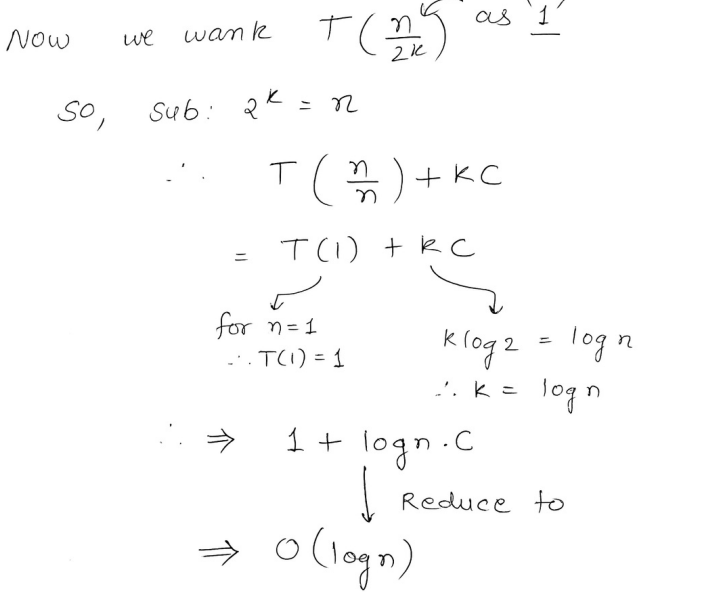
2. Master Theorem.
This theorem is faster to use than the substitution method however it cannot be applied to all recurrence relations .
There are certain conditions which need to be fulfilled for the Master Theorem to be fulfilled.
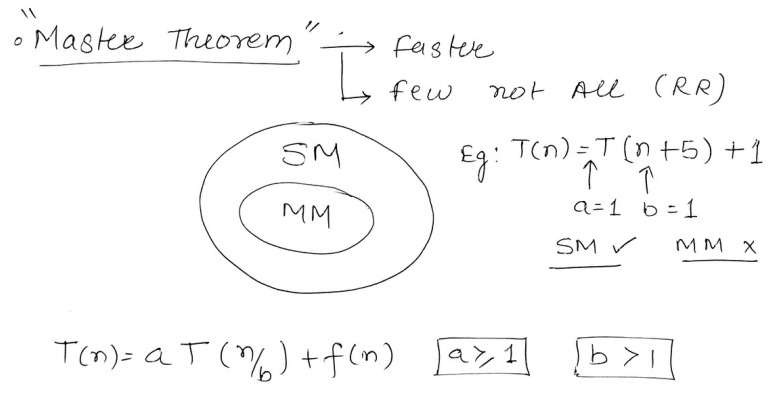
So if the recurrence relation is of the type :
where and b > 1
Therefore, Master theorem can be applied to this recurrence relation.

In the problems/limitations section those are the factors which prevent Master theorem from working on a recurrence relation.
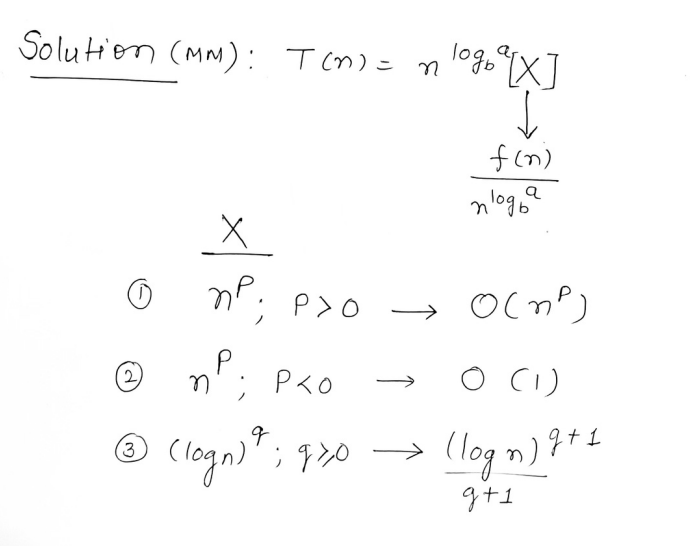
Now, we need to convert that recurrence relation to the form of
or
where if X = then it is the upper bound O() if X = , then it is linear time, O(1) if X = then it becomes