Tractable Problems
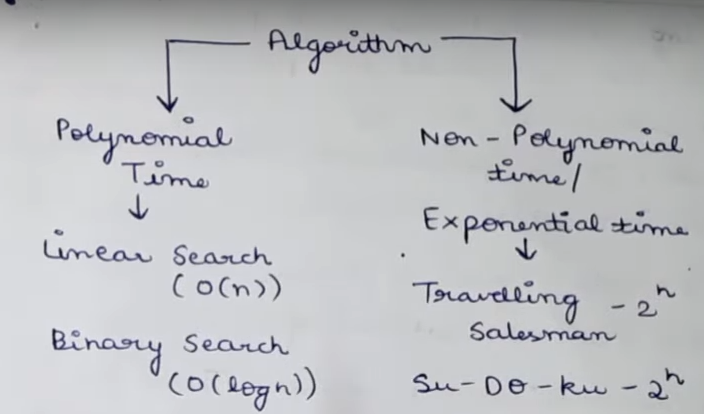
If a problem which can be solved in a polynomial time or there is an efficient algorithm which solves it in polynomial time, it is known as a tractable problem.
Examples of TP : Searching an ordered list, sorting a list.
Intractable Problems
A problem that cannot be solved in a polynomial time or there is no efficient algorithm which solves it in polynomial time, it is known as a intractable problem.
Examples of IP : List of all permutations of n numbers, The Tower of Hanoi problem.
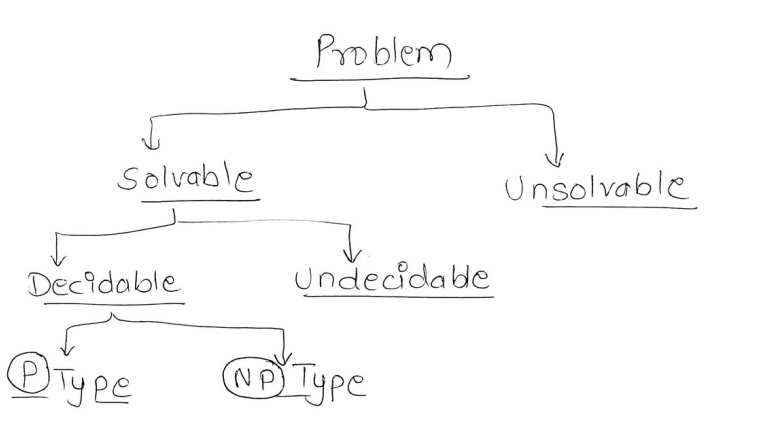
Computational Problems
There are computational problems that cannot be solved by algorithms even with unlimited time.
For example : The Turing Halting problem
Following these problems we can classify the problems into 4 classes :
- P-class
- NP-class
- NP-hard
- NP-complete
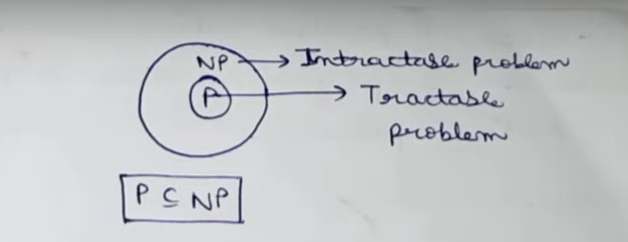
P-Class problems
A program which can solved in polynomial time is known as a P-class problem.
Example :
- Sorting
- Searching
- Shortest Path algorithms
NP-Class (non-deterministic polynomial time) problems
A problem which cannot be solved in polynomial time but can be verified in polynomial time is known as a NP-Class problem
Example :
- 0/1 Knapsack problem
- TSP
- sudoku solving problem etc.
Reduction


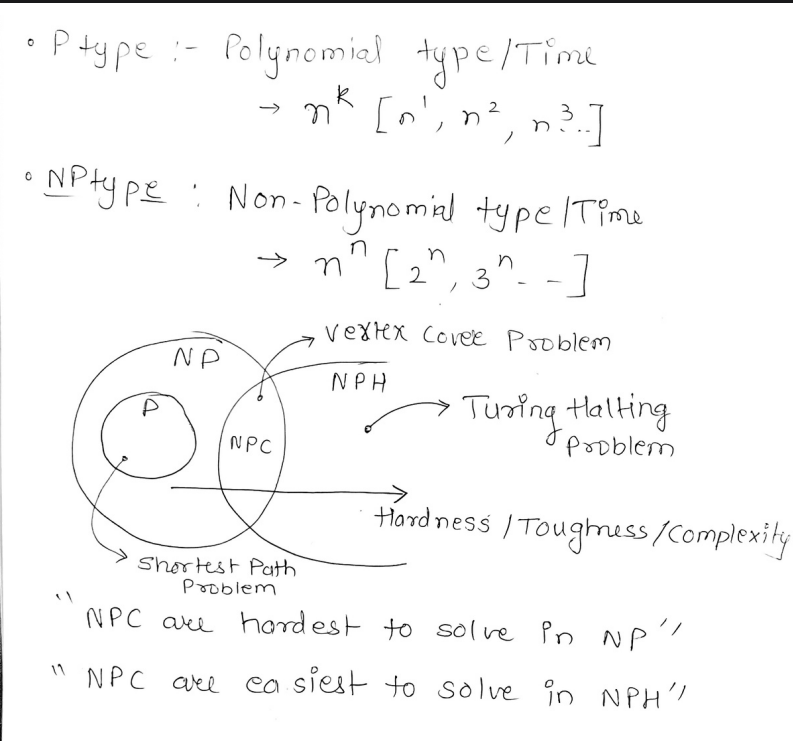
NP-Hard Problems
A problem is said to be a NP-Hard problem if every problem in NP can be polynomially reduced to it.
Example : Vector cover, TSP
NP-Complete Problems

A problem is said to be NP-Complete if it is in NP and it is NP-Hard.
The class of NP-Complete problems is the intersection of the NP and NP-hard class
Example : Graph coloring problem, Longest Path problem.

Cook’s Theorem
Cook’s Theorem is a foundational result in computational complexity theory, =established by Stephen Cook in 1971. The theorem states that the Boolean satisfiability problem (SAT) is NP-complete.= This was the first problem to be proven NP-complete, and it demonstrated that SAT is at least as hard as any other problem in the complexity class NP. Here is a more detailed breakdown of Cook’s Theorem:
-
SAT is in NP: Cook first showed that the SAT problem is in NP. =This means that given a Boolean formula, if there exists a satisfying assignment (a set of variable assignments that makes the formula true), then this assignment can be verified in polynomial time=.
-
NP-Completeness of SAT: Cook then =proved that any problem in NP can be reduced to SAT in polynomial time. This implies that if there is a polynomial-time algorithm for solving SAT, then there is a polynomial-time algorithm for solving any problem in NP=. In other words, SAT is NP-complete because it is both in NP and as hard as any problem in NP.
Implications of Cook’s Theorem
-
Foundation of NP-Completeness: Cook’s Theorem introduced the concept of NP-completeness, providing a framework for identifying other NP-complete problems. If any NP-complete problem can be solved in polynomial time, then all problems in NP can be solved in polynomial time (i.e., P=NP).
-
Reduction Technique: The theorem established the technique of polynomial-time reductions, which is used to show that one problem is at least as hard as another. This technique is crucial for proving that various problems are NP-complete.
Formal Statement of Cook’s Theorem
In formal terms, Cook’s Theorem can be stated as follows:
- The Boolean satisfiability problem (SAT) is NP-complete.
- For any problem L in NP, there exists a polynomial-time reduction from L to SAT.
Cook’s Theorem remains a cornerstone of theoretical computer science, guiding research in algorithm design, complexity theory, and computational problem-solving.
Applications of Cook’s Theorem (just see the header part only) :
1. Identification of NP-Complete Problems
Cook’s Theorem provides a foundation for identifying other NP-complete problems through polynomial-time reductions. Once SAT was proven to be NP-complete, researchers could show that other problems are NP-complete by reducing SAT to these problems in polynomial time.
2. Complexity Theory and Classification of Problems
Cook’s Theorem is central to complexity theory, which studies the inherent difficulty of computational problems. It helps classify problems into different complexity classes (e.g., P, NP, NP-complete) and understand their relationships. This classification is crucial for understanding the limits of efficient computation.
3. Algorithm Development and Optimization
Understanding that a problem is NP-complete guides researchers and practitioners in algorithm development. Knowing that a problem is unlikely to have a polynomial-time solution motivates the development of approximation algorithms, heuristics, and specialized algorithms for practical cases.
4. Cryptography
Many cryptographic protocols rely on the difficulty of solving NP-complete problems. For example, the security of certain cryptographic systems is based on the assumption that specific NP-complete problems cannot be solved efficiently, ensuring data security.
5. Computational Intractability in Various Fields
Cook’s Theorem has applications in fields such as operations research, artificial intelligence, bioinformatics, and economics, where many practical problems are NP-complete. Understanding the NP-completeness of these problems helps in designing realistic approaches to tackle them.
6. SAT Solvers and Practical Applications
SAT solvers are tools designed to solve instances of the SAT problem efficiently in practice. Despite the theoretical NP-completeness of SAT, modern SAT solvers can handle large and complex instances, making them useful in various applications, including:
- Hardware and Software Verification: Ensuring the correctness of hardware designs and software programs.
- Automated Planning and Scheduling: Solving planning problems in artificial intelligence and operations research.
- Constraint Satisfaction Problems: Addressing problems in areas like scheduling, resource allocation, and configuration.
7. Reductions and Problem Transformation
Cook’s Theorem underpins the concept of polynomial-time reductions, a powerful technique for transforming one problem into another. This technique is widely used to show the hardness of problems, design algorithms, and develop new problem-solving approaches.
8. Theory of Computation and Teaching
Cook’s Theorem is a fundamental topic in theoretical computer science and is a staple in computer science education. It helps students and researchers understand the theoretical limits of computation and the nature of computational problems.